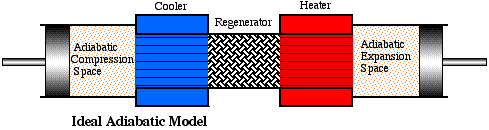
In the previous section we considered an ideal Stirling engine model in which the compression and expansion spaces were maintained at the respective cooler and heater temperatures. This led to the paradoxical situation that neither the heater nor the cooler contributed any net heat transfer over the cycle and hence were redundant. All the required heat transfer occurred across the boundaries of the isothermal working spaces. Obviously this cannot be correct, since the cylinder walls are not designed for heat transfer. In real machines the working spaces will tend to be adiabatic rather than isothermal, which implies that the net heat transferred over the cycle must be provided by the heat exchangers. We thus consider an alternative ideal model for Stirling cycle engines, the Ideal Adiabatic model.

As before the engine is configured as a five component serially connected model having perfectly effective heat exchangers (including the regenerator) and in this respect is similar to the Ideal Isothermal model defined previously. However both the compression and expansion spaces are adiabatic, in which no heat is transferred to the surroundings. In the following diagram we define the Ideal Adiabatic model nomenclature. Thus we have a single suffix (c, k, r, h, e) representing the five cells, and a double suffix (ck, kr, rh, he) representing the four interfaces between the cells. Enthalpy is transported across the interfaces in terms of a mass flow rate m' and an upstream temperature T. The arrows on the interfaces represent the positive direction of flow, arbitrarily defined from the compression space to the expansion space.

Notice from the temperature distribution diagram that the temperature in the compression and expansion spaces (Tc and Te) are not constant, but vary over the cycle in accordance with the adiabatic compression and expansion occurring in the working spaces. Thus the enthalpies flowing across the interfaces ck and he carry the respective adjacent upstream cell temperatures, hence temperatures Tck and The are conditional on the direction of flow and are defined algorithmically as follows:
if mck' > 0 then Tck = Tc else Tck = Tk
if mhe' > 0 then The = Th else The = Te
In the ideal model there is no gas leakage, the total mass of gas M in the system is constant, and there is no pressure drop, hence p is not suffixed and represents the instantaneous pressure throughout the system.
Work W is done on the surroundings by virtue of the varying volumes of the working spaces Vc and Ve, and heat Qk and Qh is transferred from the external environment to the working gas in the cooler and heater cells, respectively. The regenerator is externally adiabatic, heat Qr being transferred internally from the regenerator matrix to the gas flowing through the regenerator void volume Vr.
The general approach for deriving the equation set is to apply the equations of energy and state to each of the cells. The resulting equations are linked by applying the continuity equation across the entire system. Consider first the energy equation applied to a generalised cell which may either be reduced to a working space cell or a heat exchanger cell. Enthalpy is transported into the cell by means of mass flow mi' and temperature Ti, and out of the cell by means of mass flow mo' and temperature To. The derivative operator is denoted by d, thus for example dm refers to the mass derivative dm/dθ, where θ is the cycle angle.
The word statement of the energy equation for the
working gas in the generalised cell is
Mathematically,
this word statement becomes
dQ + (cp Ti mi' - cp To mo') = dW + cv d(m T)
where cp and cv are the specific heat capacities of the gas at constant pressure and constant volume respectively. This equation is the well known classical form of the energy equation for non steady flow in which kinetic and potential energy terms have been neglected.
We assume that the working gas is ideal. This is a reasonable assumption for Stirling engines since the working gas processes are far removed from the gas critical point. The equation of state for each cell is presented in both its standard and differential form as follows
p V = m R T
dP / p + dV / V = dm / m + dT / T
The starting point of the analysis is that the total mass of gas in the machine is constant, thus:
mc + mk + mr + mh + me = M
Substituting for the mass in each cell from the ideal gas law above
p (Vc / Tc + Vk / Tk + Vr / Tr + Vh / Th + Ve / Te) / R = M
where for the assumed linear temperature profile in the regenerator the mean effective temperature Tr is equal to the log mean temperature difference Tr = (Th - Tk) / ln(Th / Tk). Solving the above equation for pressure
p = M R /(Vc / Tc + Vk / Tk + Vr / Tr + Vh / Th + Ve / Te)
Differentiating the equation for mass above
dmc + dmk + dmr + dmh + dme = 0
For all the heat exchanger cells, since the respective volumes and temperatures are constant, the differential form of the equation of state reduces to
dm / m = dp / p
dm = dp m / p = (dp / R) V / T
Substituting in the mass equation above
dmc + dme + (dp / R) (Vk / Tk + Vr / Tr + Vh / Th) = 0
We wish to eliminate dmc and dme in the above equation so as to obtain an explicit equation in dp. Consider the adiabatic compression space (dQc = 0).
Applying the above energy equation to this space we obtain
-cp Tck mck' = dWc + cv d(mc Tc)
From continuity considerations the rate of accumulation of gas dmc is equal to the mass inflow of gas given by -mck', and the work donw dWc is given by p dVc, thus
cp Tck dmc = p dVc + cv d(mc Tc)
Substituting the ideal gas relations p Vc = mc R Tc, cp - cv = R, and cp / cv = γ, and simplifying
dmc = (p dVc + Vc dp / γ) / (R Tck)
Similarly for the expansion space
dme = (p dVe + Ve dp / γ) / (R The)
Substituting for dmc and dme above and simplifying
From the differential form of the equation of state above we obtain relations dTc and dTe
dTc = Tc (dp / p + dVc / Vc - dmc / mc)
dTe = Te (dp / p + dVe / Ve - dme / me)
Applying the energy equation above to each of the heat exchanger cells (dW = 0, T constant) and substituting for the equation of state for a heat exchanger cell (dm = dp m / p = (dp / R) V / T)
dQ + (cp Ti mi' - cp To mo') = cv T dm = V dp cv / R
Thus for the three heat exchanger cells we obtain
dQk = Vk dp cv / R - cp (Tck mck' - Tkr mkr')
dQr = Vr dp cv / R - cp (Tkr mkr' - Trh mrh')
dQh = Vh dp cv / R - cp (Trh mrh' - The mhe')
We note that since the heat exchangers are isothermal and the regenerator is ideal, Tkr = Tk and Trh = Th.
Finally the work done in the compression and expansion cells is given by
W = Wc + We
dW = dWc + dWe
dWc = p dVc
dWe = p dVe
The final set of pertinent differential and algebraic equations required for solution is gathered in the Equation Summary.
______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License