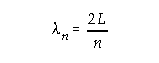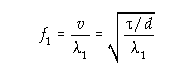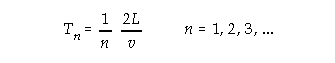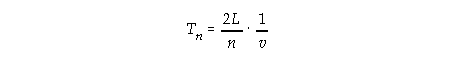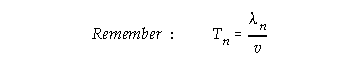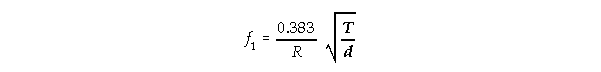Mechanical Waves

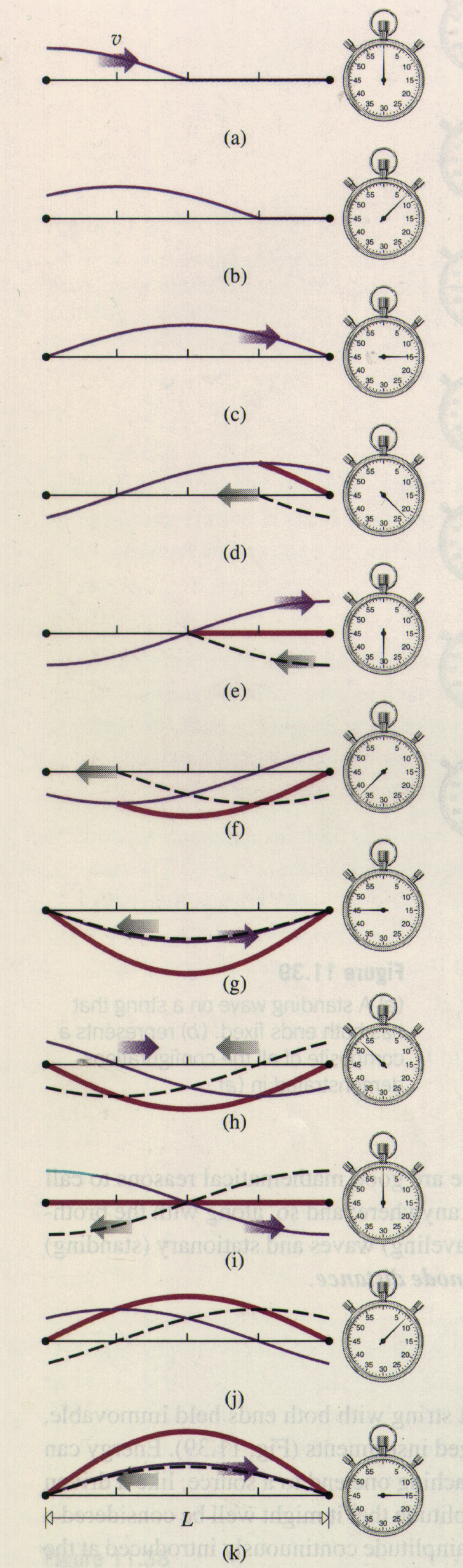
Standing Waves Reflection of a Wave - A standing Wave A wave enters from the left (a) and is reflected (dashed) from the termination point on the right (d). Now there are two overlapping waves that combine to form a standing wave (red), oscillating (g through k) in place. in-phase standing wave This occurs when wave makes one complete trip along the length of the string (distance = 2 L) in the same time as one period of oscillation. 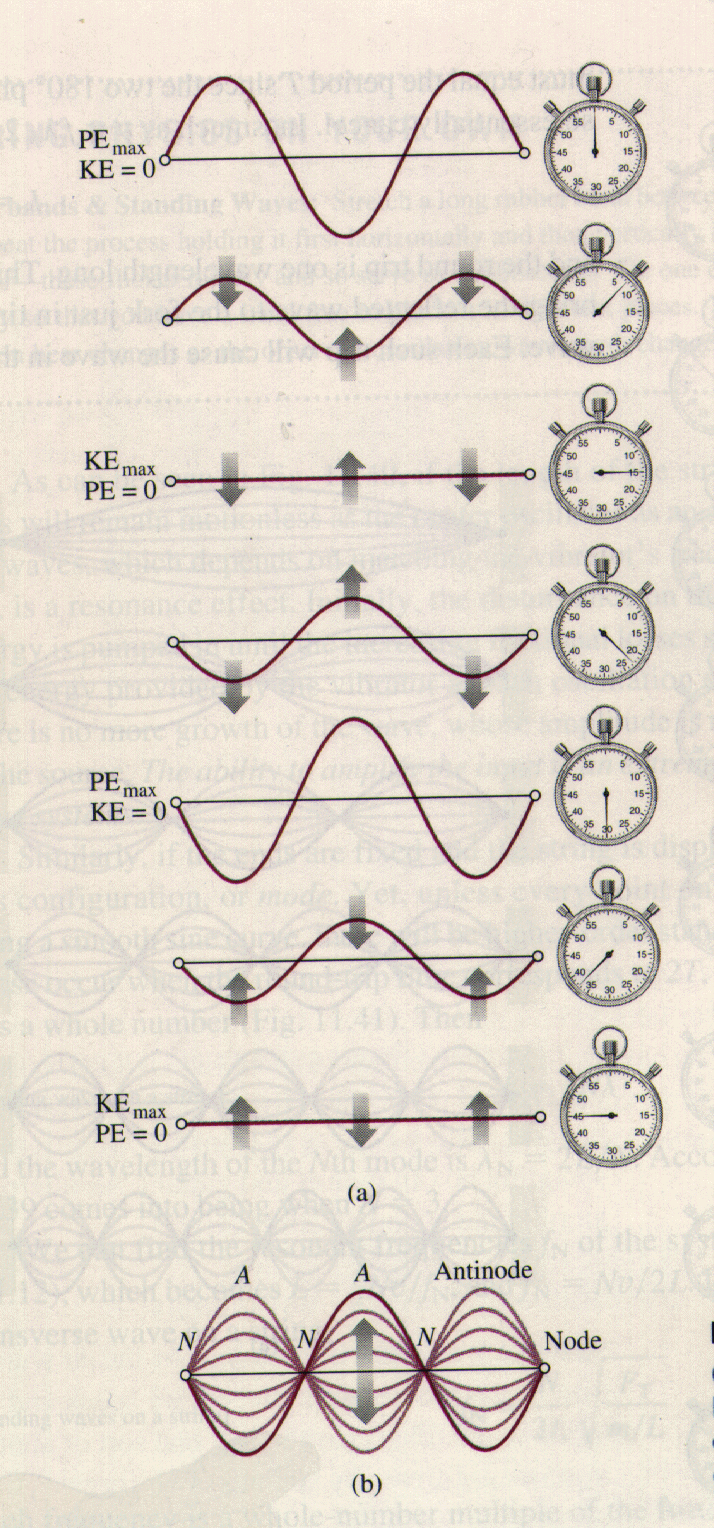Standing Wave on a String (a) A standing wave on a string that has both ends fixed. (b) represents a composite of all the configurations demonstrated in (a). 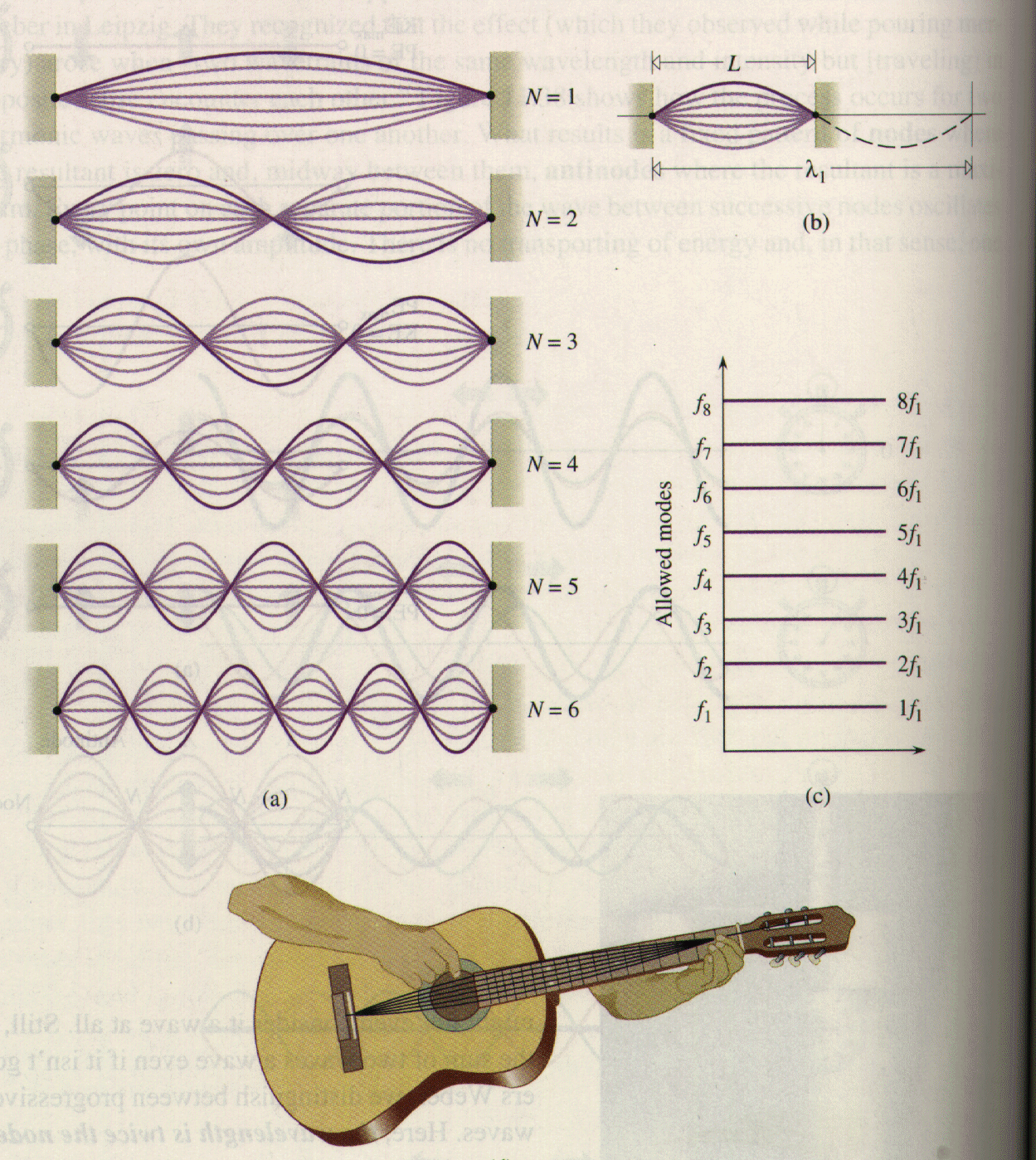Wavelength: n = 1,2, 3, . . . 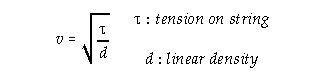All harmonics are produced Wave velocity: Frequency: fn = n f1 : n = 1, 2, 3, . . . Period of vibration: Standing Waves in 2D (drum) f1 : fundamental frequency depends on radius R of drum tension of membrane T material of membrane d Overtones: f2 = 1.59 f1 f3 = 2.13 f1

Ch. Elster
Aug 26 14:27:03 EDT 2019