Musics and Musical Instruments

Musical Scales Pythagoras (1200 B.C.) found: 2 strings [1 twice the length of the other] octave 2 strings [length ratio 3/2] fifth 2 strings [length ratio 4/3] fourth Going up a `fifth' each time he could get a whole musical scale. One octave : from A --> A --> A A B C D E F G A B C D E F G A B C D E F G . . . One fifth : C --> G --> D --> A --> ... Eventually, one comes back to same note. C . . . . 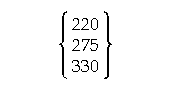---> C This is known of the "circle of fifths" (used in jazz) Pythagorean Scale NOT what we use today Example: 220 Hz = fundamental 440 Hz = 1 octave 660 Hz = a "fifth" above 440 Hz 660 Hz = 440 * 3/2 a fifth higher than 220 Hz: 220 * 3/2 = 330 Hz a third higher than 220 Hz: 220 * 5/4 = 275 Hz played at once => major chord Musical Intervals Interval frequency 1. Pair of matching harmony Unison f1 ; f2 = f1 f1 with f2 Octave f1 ; f2 = 2f1 f2 with 2f1 Fifth f1 ; f2 = 3/2 f1 2f2 with 3f1 Fourth f1 ; f2 = 4/3 f1 3f2 with 4f1 Third (major) f1 ; f2 = 5/4 f1 4f2 with 5f1 Whole tone f1 ; f2 = 1.123 f1 no match Semitone f1 ; f2 = 1.0595 f1 no match Pythagorean Scale --> the third is off! The Just Scale was created to fix this make a major chord above make a major chord below continue until all notes are found Problem: has different sizes whole steps Fix: Smooth out using the Equal Tempered Scale