unpolarized

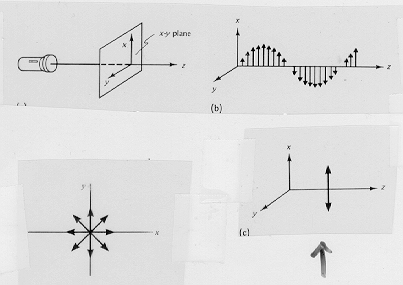
Most natural light, such as sunlight, moonlight, lightbulb light (but not all star light) is unpolarized.

linearly polarized

in the x-direction (part (b) and (c) of the figure). Similarly, a wave whose electric field is always parallel to the y-axis is linearly polarized in the y-direction.
Suppose the wave is linearly polarized in some other direction, say at an angle of 45 deg between the the x- and y-axes.

A polarizing filter can be used in two different ways. It can be used as polarizer, because it tansmits only one component of the polarization. Incident unpolarized light striking a polarizing filter results in polarized transmitted light.
Alternatively, it can be used as analyzer. One can detect the presence of polarized light with it, and the direction of polarization, once the filter is calibrated.`

The following figure shows a set-up using two polarizing filters, one as polarizer and one as analyzer.

• (a) Incident light strikes the firest polarizing filter (polarizer). The light passes through the polarizer, then strikes the second polarizing filter (analyzer). The amount of light that passes through the analyzer depends on the relative angle of the polarizer and analyzer.
• (b) Crossed polarizer and analyzer:
  Incident unpolarized light striking a vertically oriented polarizer produces vertically polarized light, which is not passed by a horizontally oriented analyzer.
• (c) Parallel polarizer and analyzer:
  The same as in (b), but now the vertically polarized light is passed by the vertically oriented analyzer.
• (d) Now the anlayzer, oriented at an intermediate angle, passses only that component of the intermediate light jpolarized at the same angle. A weaker transmitted light results.

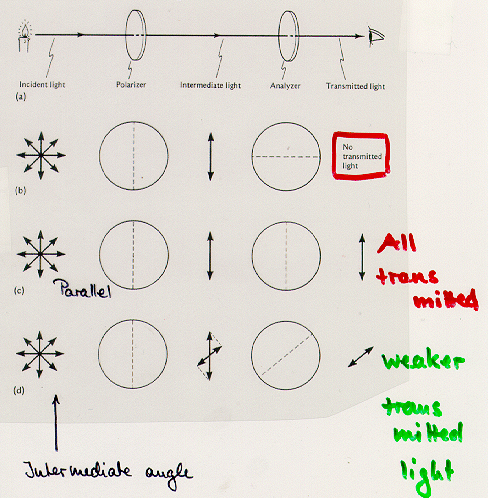
Ponder: What transmitted light results if the polarizer is oriented horizontally in the figure?

Clearly, there is not always a polarizer available to polarize light. However, there are other mechanisms due to which unpolarized light can become polarized.

For the blue, Rayleigh scattered light this means that he blue light is linearly polarized for light coming from points in the sky 90 deg away from the sun. However, the light coming from diretions near the sun or opoosite the sun is unpolarized. For regions inbetween it is partially polarized, a mixture of polarized and unpolarized light.
If there are large particles in the air (as in smog) the forces within within them may cause the charges to oscillate in other directons than that of the electric field of the incident wave, so the scattered light is polarized less, if at all. Repeated scattering, as in clouds, causes the light to come out polarized in all directions, that is unpolarized. So light from clouds is not polarized.

Because of the polarization of the light from the blue sky, a poperly oriented polarizing filter in front of your camera can block out that that light, increasing hte contrast beween the sky and the white clouds as in this photograph of taken in the middle of the day in Mexico.

A wave with its E-field perpendicular to the plane-of-incidence reflecting and refracting at an interface. Electrons then oscillate perpendicular to the plane-of-incidence and reradiate light perpendicular to that plane.

 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
  If the incident E-field is linearly polarized in the plane-of-incidence, something rather different happens to the reflected wave.

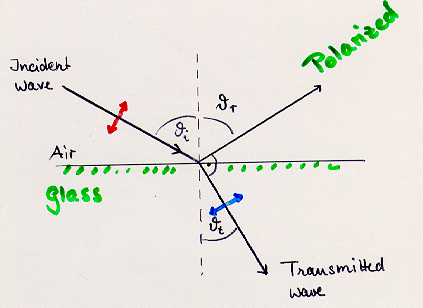
When light coming from air strikes a smooth glass surface at an angle of incidence, , it wiggles the charges at the surface of the glass. There is a direction, , in which the radiation emitted from these charges is in phase. This is the reflected beam, with . Similarly, there is a direction (the transmitted direction), of conctructive interference between the incident radiation and that from the glass atoms. This is the transmitted beam given by Snell's law.

The figure is drawn for a special case, where the transmitted and reflected rays happen to be at right angles to each other and the oscillations of the E-field occur in the plane-of-incidence. If this is the case, the reflected light will be polarized.

How can this be explained? For the specific situation given in the figure and light polarized in the plane of the figuer, the electric field in the glass, and thus the direction in which the charges oscillate there, is perpendicular to the transmitted ray. It is the radiation from these oscillating charges, that produces the reflected ray. Because light is transverse, these charges cannot radiate along their direction of oscillation. Hence there cannot be a reflected ray perpendicular to the transmitted ray. Thus, the intensity of the reflected ray is zero for this special angle of incidence, called

Brewster's angle

Thus, if an unpolarized beam arrives at the Brewster's angle of incidence, only one component of polarization is reflected. The reflected light is then linearly polarized. At nearby angles this is almost true, i.e. of light polarized in the plane of the figure, very little is reflected. Hence, the reflected light is partially polarized, consisting of a large component of one polarization and a small component of the other. Since one often looks at objects at angles near Brewster's angle, much of the reflected light one sees is polarized. Water surfaces or snow are especially good reflectors of light, so one can expect that the reflected light has a large polarized component. This can be seen in the two photographs shot in snow. For the right one a polarizing filter was used, for the left one not.

The situation is different for metals. Since in metals electrons are moving quite freely parallel to the surface, they can radiate in all directions away from the surface and can hence create reflected beams of both polarizations, which means the light reflected from metal surfaces is not polarized.

When linearly polarized light passes through an optically active material, its direction of polarization is rotated. The angle through which the polarization is rotated depends on the thickness of the material and the wavelength of the light in that material. If you put some optically active material between a polarizer and an analyzer, then, depending on the orientation of the analyzer (compared to that of the polarizer), different colors will be removed from the transmitted light.