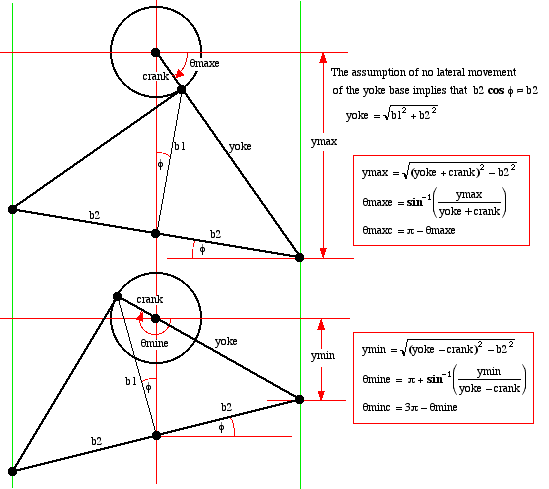
We now consider the minimum and maximum displacements of the compression and expansion pistons. Notice that they respectively occur when the crank arm lines up with the yoke edge.
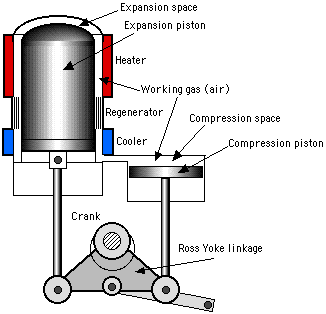
The Ross Yoke-drive engine was invented by Andy Ross and is unique in that there is virtually no side movement of the two piston connecting rods, and thus no side forces on the pistons. Matt Keveney did an excellent animation of the Ross Yoke-drive engine showing clearly the principle of operation of this unique design.
In order to begin a simulation of the performance of
the Ross Yoke-drive engine we need to derive equations for the volume
variations Vc and Ve as well as the volume derivatives dVc
and dVe as functions
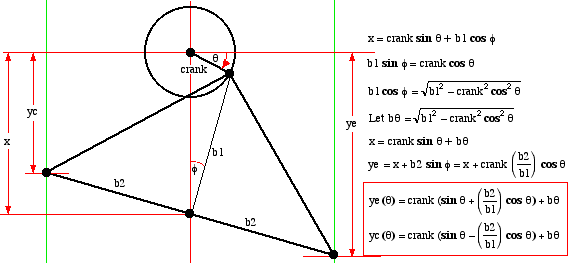
of the crankangle θ. The diagram below shows the two basic
components of the Ross Yoke-drive - the crank and the yoke. The
crankangle θ has a positive clockwise rotation starting from the
horizontal crank arm position as shown. Let yc and ye respectively
represent the displacements of the compression and expansion pistons,
and x the displacement of the yoke pin at the center of the yoke
base, all with respect to the crank axle. The basic assumption of the
analysis is that the lateral movement of the connecting rods
connected to the two extremeties of the yoke, as well as the yoke pin
at the center of the yoke, is negligible.
We
now consider the minimum and maximum displacements of the compression
and expansion pistons. Notice that they respectively occur when the
crank arm lines up with the yoke edge.
Thus for compression, expansion piston areas Ac, Ae, and clearence volumes Vclc, Vcle, the complete set of equations for evaluating the volumes Ve, Vc and the volume derivatives dVe, dVc are given by:

______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by
Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License