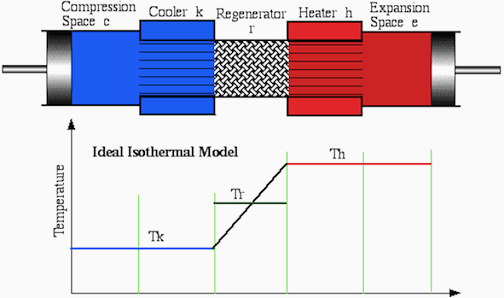

We now consider the Ideal Isothermal model from the point of view of energy flow. Heat transfer to and from the external environment occurs at the cold and hot temperatures Tk and Th respectively. Typically, Stirling engines will have separate heater and cooler heat exchangers, as indicated in the above figure. To investigate the heat transfer to these spaces, it is necessary to consider the working gas energy equation.
A generalised cell is shown below which may either be
reduced to a working space cell or a heat exchanger cell. Enthalpy is
transported into the cell by means of mass flow mi' and temperature
Ti, and out of the cell by means of mass flow mo' and temperature To.
The derivative operator is denoted by d,
thus for example dm
refers to the mass derivative dm/dθ,
where θ is the cycle angle.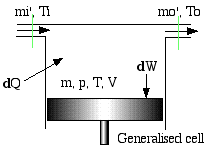
The
word statement of the energy equation for the working gas in the
generalized cell is
Recall
from thermodynamics
that for an ideal gas, enthalpy and internal energy are
functions of temperature only, thus:
specific enthalpy h = cp T
specific internal energy u = cv T
where cp and cv are the specific heat capacities of the gas at constant pressure and constant volume respectively.
Thus substituting in the above word statement we obtain
dQ + (cp Ti mi' - cp To mo') = dW + cv d(m T)
This equation is the well known classical form of the energy equation for non steady flow in which kinetic and potential energy terms have been neglected. In the isothermal model for the compression and expansion spaces, as well as for the heater and cooler, we have Ti = To = T, a constant value. Furthermore, from mass conservation considerations, the difference in the mass flow (mi' - mo') is equal to the rate of mass accumulation within the cell dm. The above equation thus simplifies to
dQ + cp T dm = dW + cv T dm
dQ = dW - R T dm
where for the assumed ideal gas, the gas constant R = cp - cv.
The net heat transferred to the working gas over the cycle Q is given by cyclic integration of dQ. However, the implicit assumption that cyclic steady state has been attained implies that the cyclic change in mass of the working gas (m) is zero for each of the cells. Thus applying the above equation to each of the isothermal cells and integrating over the cycle, we obtain for the working spaces
Qc = Wc
Qe = We
Similarly, for the heat exchanger spaces, in which no work is done
Qk = 0
Qh = 0
Of course, for the ideal regenerator Qr = 0. This is because all heat exchange between the regenerator matrix and the working gas is internal - there is no external heat transferred between the regenerator and the environment.
This is an amazing result - it implies that the heat exchangers are redundant, all the required external heat transfer occurring across the boundaries of the working spaces. This apparent paradox is a direct result of the isothermal model in which the compression and expansion spaces are maintained at the respective cooler and heater temperatures. Obviously this cannot be correct, since the cylinder walls are not designed for heat transfer. In real machines the working spaces will tend to be adiabatic rather than isothermal, which implies that the net heat transferred over the cycle must be provided by the heat exchangers.
We thus consider an alternative ideal model for Stirling cycle engines, the Ideal Adiabatic model, which will be developed in Chapter 4.
______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by
Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License