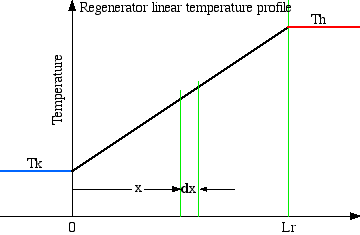
In order to correctly evaluate the mass of gas in the regenerator void space, the lengthwise distribution of the gas temperature must be known. We will assume that the ideal regenerator has a linear temperature profile between the cold temperature Tk and the hot temperature Th, as shown in the following figure.

Thus the temperature profile in the regenerator can be described by
T(x) = (Th - Tk) x / Lr + Tk
where Lr is the regenerator length.
The total mass of gas mr in the regenerator void space Vr is given by
where ρ is the density. Now from the ideal gas equation of state, and for a constant free flow area Ar, we have
p = ρ R T
dVr = Ar dx
Vr = Ar Lr
Substituting for ρ, Vr, and dVr in the above equation and simplifying
Integrating and simplifying
We now define the mean effective temperature Tr of the gas in the regenerator in terms of the ideal gas equation of state
mr = Vr p / (R Tr)
Comparing the above two equations and equating Tr, we obtain
Tr = (Th - Tk) / ln(Th / Tk)
This equation gives the mean effective regenerator Tr as a function of Tk and Th, as required.
______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License