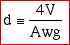
Forced convection heat transfer is fundamental to Stirling engine operation. Heat is transferred from the external heat source to the working fluid in the heater section, cyclicly stored and recovered in the regenerator, and rejected by the working fluid to the external heat sink in the cooler section. All of this is done in compact heat exchangers (large wetted area to void volume ratio) so as to limit the "dead space" to an acceptable value and thus allow for a reasonable specific power output of the engine. We find that effective heat exchange comes at a price of increased flow friction, resulting in the so-called "pumping loss". This loss refers to the mechanical power required to "pump" the working fluid through the heat exchangers, and thus reducing the net power output of the engine.
When we try to design a machine for a specific performance, we find that there are a large number of parameters involved which affect the performance-in non intuitive ways. The Scaling Parameter approach uses dimensional analysis to reduce the number of parameters to a basic set of dimensionless scaling groups, and thus allow experimental data to be used in various contexts. This is a standard technique in forced convection heat transfer analysis and can be reviewed in many heat transfer texts. We have based our analysis on the book "Compact Heat Exchangers" by Kays & London, both the 1955 and 1964 editions. An extremely lucid discussion of the basic scaling parameters involved and their applicability to the oscillating flow conditions of Stirling engines is found in the book " The Regenerator and the Stirling Engine" by Allan Organ (1997), and in particular Chapter 3: "Heat Transfer - and the Price". In this section we assume that you are familiar with the methods of convective heat transfer analysis and we simply define and discuss the various standard dimensionless scaling parameters for each heat exchanger section in the machine, based on a basic (exhaustive) set of variables as follows:
d - the Hydraulic Diameter (m). This variable represents ratio of the two important size parameters of a heat exchanger - the void volume V and the wetted area Awg. It is defined by:
The factor 4 is included for convenience. For flow in a circular pipe (or a homogeneous bundle of circular pipes) the Hydraulic Diameter thus becomes equal to the pipe internal diameter.
Note that some researchers (e.g. Allan Organ) use the so-called Hydraulic Radius (rh) as their scaling parameter. This is simply defined as rh = V/Awg, thus d = 4 rh.
μ - the working gas dynamic viscosity (Pa s). This is defined in terms of Newtons Law of Viscosity in the section on Pumping Loss.
u - the mean bulk velocity of the flowing fluid (m / s)
ρ - the density of the working gas (kg / cu.m)
h - the convective heat transfer coefficient (W / sq.m K). This is defined in the section on Heater and Cooler Simple analysis.
k - the working gas thermal conductivity (W / m K)
cp - the working gas specific heat capacity at constant pressure (J / kg K)
This grouping is obtained by considering the ratio of the inertial forces to the viscous forces. The value of Nre determines the flow regime, whether laminar or turbulent. Both the friction factor and the heat transfer coefficient are strongly dependent on the flow regime, thus Nre is invariably used as the independent variable in the presentation of flow-friction and heat transfer data. Note that by definition Nre is always positive, independent of the direction of fluid flow.

This grouping is one of the two standard methods for the presentation of heat transfer by convection. The physical significance of Nst is that it can be related to the ratio of the convective heat transfer to the thermal capacity of the flowing fluid. It has found favour because of the ease in which it can be obtained from experimental data. Thus from an energy balance of a heated (or cooled) fluid flowing through a heat exchanger:
where
is the rate of heat transfer
is the mass flow rate
Awg is the wall/gas, or wetted area
A is the free flow area (normal to the direction onf flow)
Tw, T are the respective wall and bulk fluid temperatures
Ti, To are the respective inlet and outlet fluid temperatures
Substituting for Nst above we obtain:
Thus the value of Nst can be obtained directly from the heat exchanger dimensions and temperature measurement without reference to the fluid properties.
Another popular grouping named the "Number of Transfer Units", or NTU, can be defined from the above energy balance equation as follows:
Note that the NTU is a function of the heat exchanger dimensions and as such is not considered a fundamental heat transfer grouping in the classical sense. However formulation in terms of NTU allows a solution in terms of Nst, and thus avoids the tedium of extracting the heat transfer coefficient h. This approach is used to advantage in the section on Regenerator Simple analysis.
This grouping is obtained from the ratio of the kinematic viscosity ν = μ / ρ (sq.m / s) (also known as the momentum diffusivity) to the thermal diffusivity α = k / ρ cp (sq.m / s), and thus represents the ratio of the viscous to the thermal boundary layers. Thus for fluids having a value of Npr close to unity the classic Reynolds Analogy can be used to relate simply between flow-friction and heat transfer data. It involves three fluid properties and is thus itself a property of the fluid, and frequently appears in heat transfer data. For the range of working gases used in Stirling engines and for the temperature range of interest (about 300 to 1000 K), Npr is approximately constant at around a value of 0.7.
Developing the Reynolds Analogy, Allan Organ (in Chapter 3 of his book " The Regenerator and the Stirling Engine") shows that one can relate the Stanton Number to the friction factor Cf (defined in the section on Pumping Loss) as follows:
Nst = Cf / 2
According to Organ, "this vital result is not quantitatively exact, but serves a more valuable purpose than any precise formula by confirming the inevitable tie between friction factor and Stanton number. It warns against unrealistic expectation of increasing heat transfer without penalty of increased pumping power."
This grouping is often used as an alternative to the Stanton Number for the presentation of heat transfer data, and is usually presented in graphical form in terms of the Prandtl and Reynolds numbers (e.g. Kays & London, " Compact Heat Exchangers"). It is not an independent grouping, and can be defined as a function of the other three dimensionless groups as follows:
Nnu = Nst.Npr.Nre
In the foregoing we have not expressed the influence of temperature on the fluid properties. Both dynamic viscosity μ and thermal conductivity k vary significantly with temperature. However, since the specific heat capacity cp and Prandtl Number Npr are approximately constant over the temperature range of interest we see from the definition of Npr that it is sufficient to consider the temperature dependence of the dynamic viscosity μ. This is considered in the section on Pumping Loss.
______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License