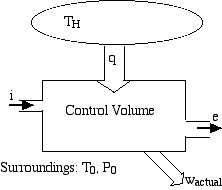
Consider the Control Volume as developed in Section a), however with the heat being transferred from a thermal source at temperature TH which is higher than the surroundings temperature T0.
Energy (First Law):
Entropy Generated (Second Law):
Since heat is exchanged with a temperature source different from the dead space temperature T0 the entropy generated is:
We now consider a reversible process between the same inlet (i) and exit (e) states and heat transfer q. This requires that reversible heat transfer q0,rev will occur from the surroundings to the control volume such that the entropy generated sgen = 0.
Thus:
Adding this new reversible heat source to the energy equation (1) above, and substituting equation (9) we obtain:
You may be confused as to how we can justify transferring heat q0 reversibly from the surroundings at T0 to the control volume at a higher temperature. This unique approach due to Sonntag and Borgnakke (Introduction to Engineering Thermodynamics, Wiley, 2001) is done for convenience in order to validate the derivation of equation (10).
In order to justify this, consider the equivalent system shown below, in which the hot source at TH is used as the heat source of a reversible heat engine, which in turn drives a heat pump to deliver the required heat q to the control volume. We will show that this system gives rise to the identical equation (10) as above.
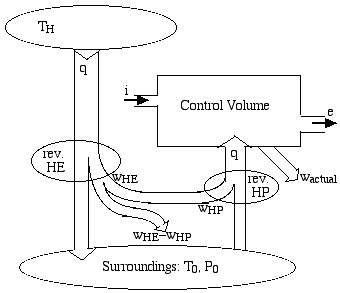
From the energy equation for the reversible heat engine (recall Chapter 5) we have:
From the diagram we see that some of this work (wHP) is used to drive the reversible heat pump. Since the temperature T of the control volume varies from the inlet to the outlet, we consider the differential energy equation for the work into the heat pump:
Integrating across the entire control volume (inlet to outlet) we obtain:
From the diagram above we see that the total reversible work available from this system is given by:
Substituting from equations (11), (12) and the initial energy equation (1) above, we have:
Simplifying equation (13) leads to equation (10) as above - QED. (Quad Erat Demonstratum - Latin for "which was to be proved" used smugly by math gurus whenever they successfully conclude a proof - usually accompanied by a condescending smile)
______________________________________________________________________________________
![]()
Engineering Thermodynamics by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License