In this chapter we consider the property values and relationships of a pure substance (such as water) which can exist in three phases - solid, liquid and gas. We will not consider the solid phase in this course.
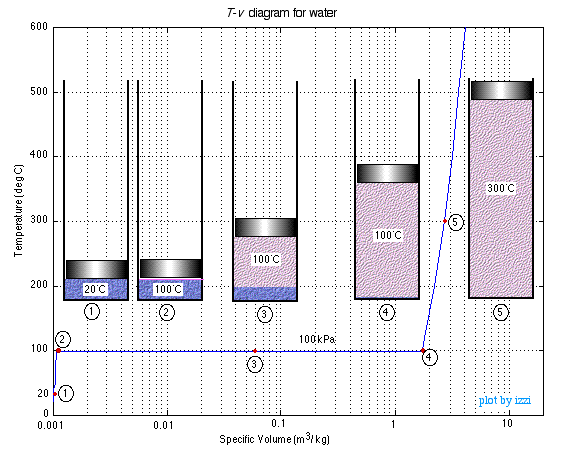
In order to introduce the rather complex phase change interactions that occur in pure substances we consider an experiment in which we have liquid water in a piston-cylinder device at 20°C and 100kPa pressure.. Heat is added to the cylinder while the pressure is maintained constant until the temperature reaches 300°C, as shown in the following T-v diagram (temperature vs specific volume):

From State (1) to State (2) the water maintains its liquid phase and the specific volume increases very slightly until the temperature reaches close to 100°C (State (2) - Saturated Liquid). As more heat is added the water progressively changes phase from liquid to water vapor (steam) while maintaining the temperature at 100°C (Saturation Temperature - Tsat) until there is no liquid remaining in the cylinder (State (4) - Saturated Vapor). If heating continues then the water vapor temperature increases (T > Tsat) and is said to be in the Superheated (State (5)).
Notice that during this entire process the specific volume of the water increased by more than three orders of magnitude, which made it necessary to use a logarithmic scale for the specific volume axis.
We now consider repeating this experiment at various pressures, as shown in the following T-v diagram:
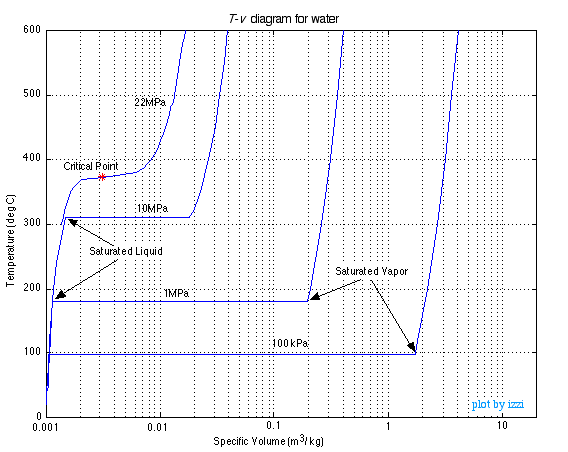
Notice that as we increase the applied pressure, the region between the saturated liquid and saturated vapor decreases until we reach the Critical Point, above which there is no clear distinction between the liquid and vapor states.
It is common practice to join the loci of saturated liquid and saturated vapor points as shown in the T-v diagram below.
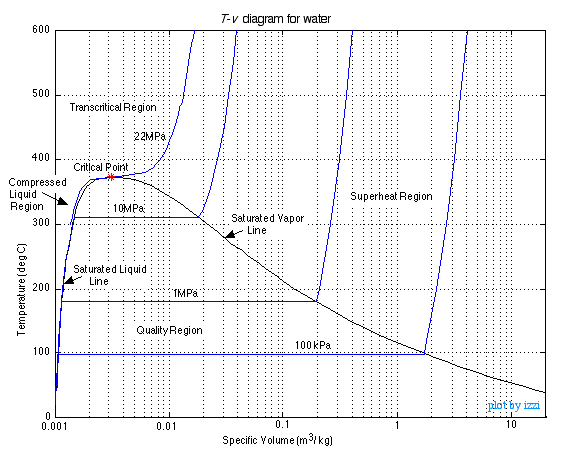
The saturation lines define the regions of interest as shown in the diagram, being the Compressed Liquid region, the Quality region enclosed by the saturation lines, and the Superheat region (which also includes the Transcritical region) to the right of the saturated vapor line and above the critical point. We will use Property Tables associated with the regions in order to evaluate the various properties. Notice that we have provided property tables of steam, Refrigerant R134a, and Carbon Dioxide, which we believe is destined to become the future refrigerant of common usage.
The Quality Region (also referred to as the Saturated Liquid-Vapor Mixture Region) is enclosed between the saturated liquid line and the saturated vapor line, and at any point within this region the quality of the mixture (also referred to as the dryness factor) is defined as the mass of vapor divided by the total mass of the fluid, as shown in the following diagram:
Notice that properties relating to the saturated liquid have the subscript f, and those relating to the saturated vapor have the subscript g. In order to evaluate the quality consider a volume V containing a mass m of a saturated liquid-vapor mixture.
Notice from the steam property tables that we have also included three new properties: internal energy u [kJ/kg], enthalpy h [kJ/kg], and entropy s [kJ/kg.K] all of which will be defined as needed in future sections. At this stage we note that the 3 equations relating quality and specific volume can also be evaluated in terms of these three additional properties.
The above discussion was done in terms of the T-v diagram, however recall from Chapter 1 when we defined the State Postulate that any two independent intensive properties can be used to completely define all other intensive state properties. It is often advantageous to use the P-v diagram with temperature as the parameter as in the following diagram:
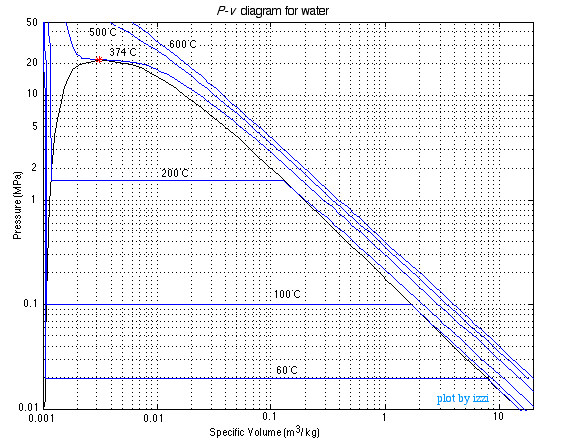
Notice that because of the extremely large range of pressure and specific volume values of interest, this can only be done on a log-log plot. This is extremely inconvenient, so both the T-v and the P-v diagrams are normally not drawn to scale, however are sketched only in order to help define the problem, which is then solved in terms of the steam tables. This approach is illustrated in the following solved problems.
Solved Problem 2.1 - Two kilograms of water at 25°C are placed in a piston cylinder device under 100 kPa pressure as shown in the diagram (State (1)). Heat is added to the water at constant pressure until the piston reaches the stops at a total volume of 0.4 m3 (State (2)). More heat is then added at constant volume until the temperature of the water reaches 300°C (State (3)). Determine (a) the quality of the fluid and the mass of the vapor at state (2), and (b) the pressure of the fluid at state (3).
Step 1: Always draw a complete diagram of the states and processes of the problem and include all the relevant information on the diagram. In this case there are three states and two processes (constant pressure and constant volume).
Step 2: In the case of a closed system with a phase change fluid, always sketch a T_v or P_v diagram indicating all the relevant states and processes on the diagram. As mentioned above this diagram will not be drawn to scale, however it will help to define the problem and the approach to solution. In the case of steam, as we determine various values from the steam tables we add these values to the diagram, typically as shown below:
Notice that the T_v diagram is based exclusively on intensive properties, hence mass is not indicated on the diagram. Thus we indicate on the diagram that in order to determine the quality at state (2) we need to first evaluate the specific volume v2, which can then be compared to the saturation values vf and vg at the pressure of 100 kPa.
Thus v2 = V / m = 0.4 [m3] / 2 [kg] = 0.2 [m3 / kg]
Concerning state (3), the problem statement did not specify that it is in the superheat region. We needed to first determine the saturated vapor specific volume vg at 300°C. This value is 0.0216 m3 / kg, which is much less than the specific volume v3 of 0.2 m3 / kg, thus placing state (3) well into the superheated region. Thus the two intensive properties which we use to determine the pressure at state (3) are T3 = 300°C, and v3 = 0.2 m3 / kg. On scanning the superheat tables we find that the closest values lie somewhere between 1.2 MPa and 1.4 MPa, thus we use linear interpolation techniqes to determine the actual pressure P3 as shown below:
Solved Problem 2.2 - Two kilograms of water at 25°C are placed in a piston cylinder device under 3.2 MPa pressure as shown in the diagram (State (1)). Heat is added to the water at constant pressure until the temperature of the fluid reaches 350°C (State (2)). Determine the final volume of the fluid at state (2).
In this example since the pressure is known (3.2 MPa) and remains constant throughout the process, we find it convenient to draw a P-v diagram indicating the process (1) - (2) as follows.
As in the previous example, on scanning the superheat tables we find that we need to interpolate between pressure P = 3.0 MPa and P = 3.5 MPa in order to determine the specific volume at the required pressure of 3.2 MPa as follows:
Problem 2.3 - A piston-cylinder device contains a saturated mixture of steam and water having a total mass of 0.5 kg at a pressure of 160 kPa and an initial volume of 100 liters. Heat is then added and the fluid expands at constant pressure until it reaches a saturated vapor state.
a) Draw a diagram representing the process showing the initial and final states of the system.
b) Sketch this process on a P-v diagram with respect to the saturation lines, critical point, and relevant constant temperature lines, clearly indicating the initial and final states.
c) Determine the initial quality and temperature of the fluid mixture prior to heating. [quality x1 = 0.182, T1 = 113.3°C]
d) Determine the final volume of the steam after heating. [0.546 m3 (546 liters)]
Note: 1000 liters - 1 m3.
Problem 2.4 - A pressure cooker allows much faster (and more tender) cooking by maintaining a higher boiling temperature of the water inside. It is well sealed, and steam can only escape through an opening on the lid, on which sits a metal petcock. When the pressure overcomes the weight of the petcock, the steam escapes, maintaining a constant high pressure while the water boils.
Assuming that the opening under the petcock has an area of 8 mm2, determine
a) the mass of the petcock required in order to maintain an operating pressure of 99 kPa gage. [80.7gm]
b) the corresponding temperature of the boiling water. [120.2°C]
Note: Assume that the atmospheric pressure is 101 kPa. Draw a free body diagram of the petcock.
On to Chapter 2b) of Pure
Substances![]()
______________________________________________________________________________________
![]()
Engineering Thermodynamics by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License