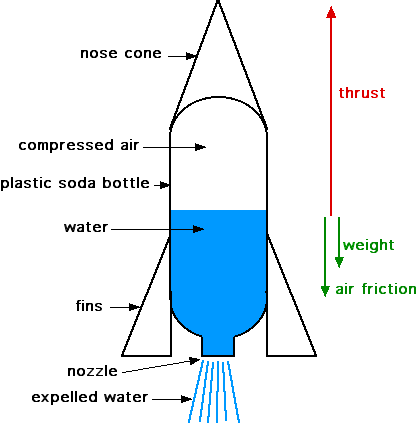
Consider the three forces applied to the rocket leading to the upward acceleration, the upward velocity and finally the height attained. These are the thrust force Fthrust, the frictional drag force Fdrag, and the weight of the rocket, as shown in the diagram below. In this exercise we wish to determine the upward velocity of the rocket throughout its flight.

We first summarize the relevant equations developed in the first exercise in Page 1 and Page 2 of the Analysis section. Note that all of this analysis is relevant to the upwards thrust phase of the rocket flight, while the water is being exhausted through the nozzle by the compressed air.
The basic rocket force equation:
The thrust force in terms of the water expelled through the nozzle:
Bernoulli's equation, relating the pressure applied by the compressd air to the velocity of the exhausting water:
Note that the resulting thrust force is twice the pressure difference times the nozzle area:
The adiabatic expansion process relating the pressure to the volume of the compressed air, which was developed in the section on Adiabatic Expansion Analysis:
The volume variation of the compressed air due to the water escaping through the nozzle is given by:
We now continue with the analysis in order to resolve the various items in equation 1 above
The total mass of the rocket (ignoring the mass of the compressed air) is given by:
The frictional drag force is given by:
where:
Cd - the coefficient of drag for the rocket (reflecting streamlining, surface roughness etc.)
Abottle - the projected area of the rocket normal to the direction of flight [m2]
- the density of the outside air [assume = 1.2 kg/m3]
u is the upwards velocity [m/s]
Note the construct u |u|, (u multiplied by the absolute value of u). This is to ensure that the drag force will always be opposed to the upward velocity, whether positive or negative, while retaining the magnitude u2.
Thus we can now evaluate the acceleration by rewriting equation 1 above as follows:
where:
a is the upwards acceleration of the rocket [m/s2]
Note that equation 10 is valid for the thrust phase. During the projectile phase when all the water has been exhausted Fthrust = 0 and the mass m reduces to Ms - the mass of the rocket solid parts (shell + payload).
Equation 10 is the differential equation for the upward velocity of the rocket as a function of time t. It cannot be solved explicity since the velocity u is deeply embedded in a nonlinear manner in the equation, hence we need to resort to a numerical solution.
We now complete the analysis by adding the equation for the height as follows:
![]()
where h is the height attained by the rocket [m]
______________________________________________________________________________________

Engineering Thermodynamics by Israel Urieli is licensed under a
Creative Commons Attribution-Noncommercial-Share
Alike 3.0 United States License