Geometrical Optics

In order to understand how lenses work, we first need to consider the effect of a spherical glass surface on light rays. For a converging surface the center of curvature lies inside the glass (the surface bulges out), and light rays incident parallel to the axis are bent towards the axis. When parallel rays go from the glass into air, they are also bent towards the axis. For a diverging surface the center of curvature lies outside the glass (surface is curved inward into the glass), and light rays incident parallel to the axis are bent away from the axis. When parallel rays go from the glass into air, they are also bent away from the axis. Convex or Converging Lens Animation Concave or Diverging Lens Animation Ray through the center of the two different lenses and through the focal point of the two lenses. Demo: Focal point of a convex lens. Try it! Focussing of parallel rays. Look at a magnifying glass! The image of converging lenses can be constructed by ray tracing . The image of diverging lenses can be constructed by ray tracing . Ray Rules for ray tracing with thin lenses. All rays incident parallel to the axis are deflected through the focal point F'. All rays through the center of the lens continue undeviated. All rays to the lens passing through the focal point F are deflected parallel to the axis Try it! Image Formation by a Converging Lens Try it! Focal point of a water drop. Try it! 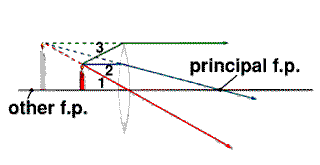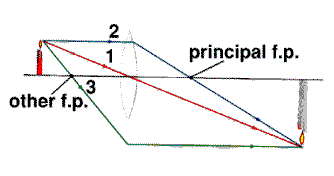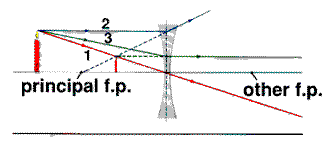Image Formation by a Diverging Lens Tutorials: Ray diagrams for concave lenses Ray diagrams for convex lenses Knowing the focal length f of a lens, we can construct the image of any object formed by that lens. Power of a lens The power of a lens is measured in diopters [D] Example: A lens of a power -2D has a focal length of 1/(-2) m or -50 cm. This means, that this lens is diverging. Diverging and converging lenses. 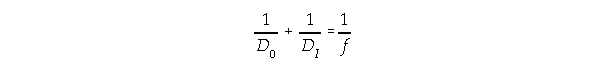Lens Equation The quantities in the lens equation are defined as follows: DO: is the distance of a given object to the center of the lens. DI: is the distance of the image of this object to the center of the lens. f: is the focal length of the lens. Entering this information into the lens equation, we get 1/(4 m) + 1/DI = 1/(2 m) ==> 1/DI = 1/(4 m) ==> DI = 4 m The Magnification of a lens is defined as: M = - DI / DO Remember: DO is + if the object is in front of the lens DO is - if the object is behind the lens DI is + if the image is on the other side of the lens compared to the object DI is - if the image is on the same side of the lens as the object f is + for a converging lens f is - for a diverging lens Tutorial: Working with the lens equation Try it! Measuring your eyeglass prescription. Retroreflectors Converging lenses can be used to make retroreflectors. Water droplets on a grass blade can act as retroreflectors. Glass bead with white paint behind them are used as retroreflectors e.g. in highway signs. Fresnel Lenses The top part of the figure shows a thick, converging lens with one flat side. The middle part of the figure shows as gray shaded area those parts of the glass of this lens that have no essential effect on the bending of light. Remember that these sections are really rings oriented perpendicular to the screen. After removing the nonessential glass and rearranging the lens, one gets the Fesnel lens shown in the bottom part of the figure. Fresnel lenses are used in spotlights. The top of an overhead projector is a Fresnel lens. Aberration We have assumed that all rays hitting our lenses or mirrors are parallel to the axis. We have ignored that the glass in a lens is dispersive. In reality, images are slightly blurred and distorted and may have colored edges. Spherical Aberation Chromatic Aberation 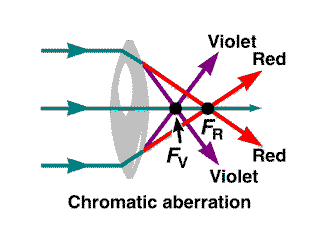A chromatic aberration produced by a converging lens. Rays of different wavelength focus at different points. (The angles are greatly exaggerated for clarity.) Examples of Chromatic aberration and how to deal with it.