
In the previous section we derived the basic set of equations which describe the Ideal Isothermal model, as shown in the following table.
Gustav Schmidt of the German Polytechnic Institute of Prague Published an analysis in 1871 in which he obtained closed form solutions of these equations for the special case of sinusoidal volume variations of the working spaces with respect to the cycle angle θ. This analysis was published in detail in the appendix of the book by Urieli & Berchowitz, "Stirling Cycle Machine Analysis", Adam Hilger 1984, and is repeated here in a condensed form for convenience.
Consider the following diagram showing the volume variations of the compression and expansion spaces (Vc and Ve) for an Alpha engine over a single cycle. Notice the phase advance angle α of the expansion space volume variation with respect to the compression space volume variation:
From the above diagram we note that the sinusoidal volume variations of the compression and expansion spaces are respectively as follows:
Vc = Vclc + Vswc (1 + cos θ) / 2
Ve = Vcle + Vswe (1 + cos(θ + α)) / 2
where Vcl and Vsw represent respectively clearence and swept volumes, and θ is the cycle angle.
Note that the following Schmidt analysis is done specifically for an Alpha type engine. For Beta or Gamma type engines we examine the equivalent sinusoidal volume variations to determine the effective Vclc, Vswc, Vcle, Vswe, and α required for this analysis.
Substituting for Vc and Ve in the pressure equation above and simplifying we obtain
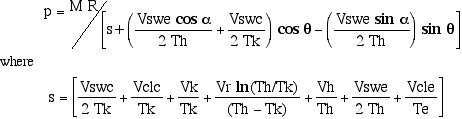
In order to simplify the pressure equation we now consider a trigonometric substitution of β and c as defined by the following right-angled triangle
Substituting for β and c in the pressure equation above and simplifying
where
φ = θ + β
b = c / s
The maximum and minimum values of pressure can now be evaluated for the extreme values of cos φ
The average pressure over the cycle is given by
From tables of integrals, this reduces to
This equation is the most convenient way of relating the total mass of working gas in the cycle to the more conveniently specified mean operating pressure.
The net work done by the engine is the sum of the work done by the compression and expansion spaces. Over a complete cycle
W = Wc + We
The volume derivatives are obtained by differentiating Vc and Ve above
Substituting these and the pressure equation into the equations for Wc and We
The solution of these integrals requires the judicious use of tables of integrals and is done in the appendix of the book by Urieli & Berchowitz, "Stirling Cycle Machine Analysis", Adam Hilger 1984. Solving these integrals we obtain:
______________________________________________________________________________________
![]()
Stirling Cycle Machine Analysis by
Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License