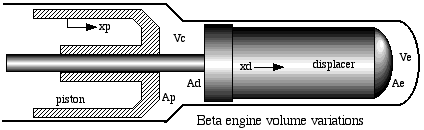
function betadrive
% Beta drive engine configuration
% Israel Urieli 1/22/08
global vclc vcle % compression,expansion clearence vols [m^3]
global vswc vswe % compression, expansion swept volumes [m^3]
global alpha % phase angle advance of expansion space [radians]
global new fid % new data file
fprintf('beta drive engine configuration\n')
if (strncmp(new,'y',1))
xpa = input('enter piston amplitude (m): ');
xda = input('enter displacer amplitude (m): ');
phid = input('enter displacer phase angle advance [degrees]: ');
dp = input('enter piston diameter (m): ');
dd = input('enter displacer diameter (m): ');
dr = input('enter displacer rod diameter (m): ');
vclc = input('enter compression space clearance volume [m^3]: ');
vcle = input('enter expansion space clearance volume [m^3]: ');
fprintf(fid, '%.3e\n', xpa);
fprintf(fid, '%.3e\n', xda);
fprintf(fid, '%.1f\n', phid);
fprintf(fid, '%.3e\n', dp);
fprintf(fid, '%.3e\n', dd);
fprintf(fid, '%.3e\n', dr);
fprintf(fid, '%.3e\n', vclc);
fprintf(fid, '%.3e\n', vcle);
else
xpa = fscanf(fid,'%e',1);
xda = fscanf(fid,'%e',1);
phid = fscanf(fid,'%f',1);
dp = fscanf(fid,'%e',1);
dd = fscanf(fid,'%e',1);
dr = fscanf(fid,'%e',1);
vclc = fscanf(fid,'%e',1);
vcle = fscanf(fid,'%e',1);
end
ap = pi*dp*dp/4; % piston area (m^2)
ad = pi*dd*dd/4; % displacer area (m^2)
ar = pi*dr*dr/4; % displacer rod area (m^2)
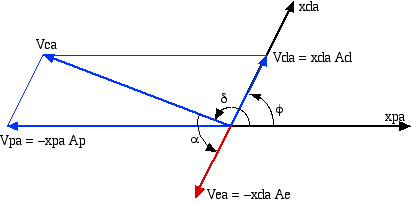
vpa = xpa*(ap - ar); % (piston - rod) volume aplitute {m^3)
vda = xda*(ad - ar); % (displacer - rod) volume amplitude(m^3)
vea = xda*ad; % displacer volume aplitute {m^3)
phi = phid*pi/180; % radians
delta = atan2(vda*sin(phi),(vda*cos(phi) - vpa));
% compression space volume to piston amplitude phase advance
vca = sqrt(vpa*vpa - 2*vpa*vda*cos(phi) + vda*vda);
% compression space volume amplitude (m^3)
vswc = 2*vca; % compression space swept volume (m^3)
vswe = 2*vea; % expansion space swept volume (m^3)
alpha = pi + phi - delta; % expansion phase angle advance (radians)
fprintf('\nbeta drive engine data summary:\n');
fprintf(' comp clearence,swept vols %.1f, %.1f [cm^3]\n', vclc*1e6,vswc*1e6);
fprintf(' exp clearence,swept vols %.1f, %.1f [cm^3]\n', vcle*1e6,vswe*1e6);
fprintf(' expansion phase angle advance %.1f[degrees]\n\n', alpha*180/pi);
%==============================================================
|