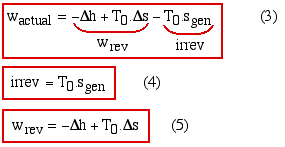
This section is mainly concerned with an attempt to develop an intuitive understanding of the exergy equations developed in the previous section, by considering reversible equivalent circuits of some common adiabatic components. We repeat equations (3), (4) and (5) developed in Chapter 7a on the exergy analysis of a control volume.
Note that the reversible work wrev will either be the maximum available output work for work producing devices, or the minimum possible input work (negative value) for work absorbing devices.
We now consider the Energy and Entropy Generation equations for adiabatic components (q = 0):
Applying all the above analysis to evaluating the Second Law Efficiencies (ηII) of adiabatic work absorbing and work producing components we obtain:
We now apply the above Second Law analysis to an adiabatic refrigeration compressor. We wish to determine the minimum work wC rev required to drive the compressor between the inlet state (1) and the exit state (2). Note that the isentropic compression that we evaluated in Chapter 6 will not provide the answer, since state (2s) is not the same as the actual state (2).
The above equations are in fact correct however we have difficulty in understanding their significance. In examining the adiabatic compressor above we cannot understand why the environment (dead space) temperature T0 features so prominently in the equations, when in fact there seems to be no obvious interaction between the adiabatic compressor and the environment. Note that as far as the adiabatic compressor is concerned we will assume that the surroundings temperature T0 is equal to the exit temperature.
In an attempt to find some intuitive meaning to these equations we consider a reversible system having the same inlet and exit states as our actual compressor. This comprises a three component system consisting of an inlet heat exchanger, a reversible heat engine and an isentropic compressor as shown below:
A typical h-s diagram for this system is shown below, in which we have used typical inlet conditions of 140kPa, -10°C and exit conditions of 700kPa, 60°C. The reversible heat engine will provide extra work to drive the compressor, absorbing its heat from the environment temperature T0 while rejecting heat to the heat exchanger. The exit state (2) from the heat exchanger has been chosen such that the compression process (2) - (3) will be isentropic.
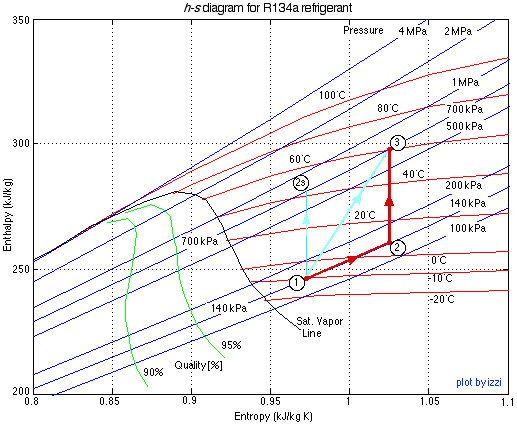
We now derive the exergy equations for the three component system above, and consider first the heat engine. Since the temperature T of the heat exchanger varies from the inlet temperature T1 to the outlet temperature T2, we use the differential energy equation form for the reversible heat engine.
Since T0 is constant, this equation can be integrated from the inlet state (1) to the outlet state (2), leading to:
This familiar final form was to be expected. The net minimum work required to drive the compressor is thus:determined as follows:
Notice that this result is identical to that shown above for the actual adiabatic compressor, since we added the heat exchanger, thus state (3) is in fact equivalent to the original state (2).
Problem 7.4 - Recall Solved Problem 6.5 in which we evaluated the Adiabatic Efficiency (ηC) of a refrigeration compressor, and determined it to be 92%. Redo this problem and determine the Second Law Efficiency (ηII) of this compressor. [92%]
We now apply the above Second Law Analysis to an adiabatic steam turbine. We wish to determine the maximum available turbine work output wT rev between the inlet state (1) and the exit state (2). We will then be able to determine the second law eficiency by comparing the actual work output to the reversible (maximum available) work output as follows:
Once again, in an attempt to find some intuitive meaning to these equations we consider a reversible system having the same inlet and exit states as the actual turbine, comprising an isentropic turbine, a heat pump pumping heat from the surroundings to the heat exchanger in the exit stream. Note that as far as the adiabatic turbine is concerned we will assume that the surroundings temperature T0 is equal to the exit temperature.
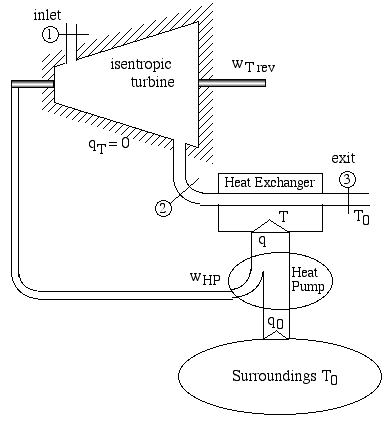
The h-s diagram for this system is shown below, in which we have chosen as an example a steam turbine having inlet conditions 6MPa, 600°C, and outlet conditions 50kPa, 100°C.
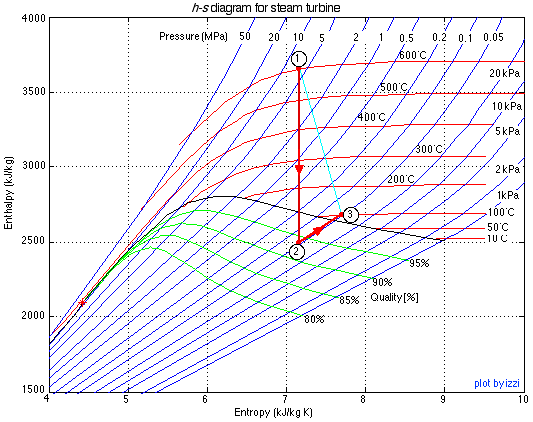
Notice from the h-s diagram that the heat exchanger temperature varies from the saturation temperature at 50 kPa (81°C) to 100°C at state (3). In order to accommodate that change we develop the differential form of the heat pump as follows:
Since T0 is constant, this differential equation can be integrated from state (2) to state (3).
We can then subtract the work provided to the heat pump from the output work of the turbine leading to the final form of the maximum available work, as follows:
Notice that this result is identical to that shown in the box above for the actual adiabatic turbine, since state (3) is in fact equivalent to the original state (2).
Problem 7.5 - Recall Solved Problem 6.1 in which we evaluated the Adiabatic Efficiencies (ηT) of both the High Pressure and the Low Pressure steam turbines of the supercritical steam power plantand found them to be 77% and 90% respectively. Redo this problem and determine the respective Second Law Efficiencies (ηII) of both turbines. [77%, 90%]
______________________________________________________________________________________
![]()
Engineering Thermodynamics by Israel
Urieli is licensed under a Creative
Commons Attribution-Noncommercial-Share Alike 3.0 United States
License