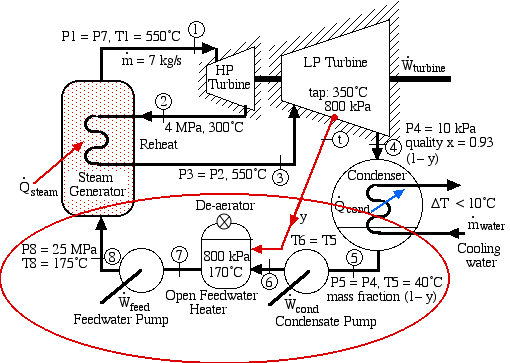
Recall the supercritical steam power plant of Solved Problem 4.2 in Chapter 4b in which the Feedwater pump is required to pump the liquid from 800kPa, 170°C to 25 MPa, as in the following figure:
In this problem we wish to determine the Adiabatic Efficiency of the feedwater pump (ηP) defined as the isentropic pump work divided by the actual pump work required to drive the pump. [ηP = 82%]
Solution Approach:
Again we are surprized to see that the feedwater pump causes the liquid to undergo a significant temperature rise of 5°C. We usually consider liquid water to be incompressible, thus pumping it to a higher pressure does not result in an increase of its temperature. However on a recent visit to the Gavin Power Plant we discovered that at 25MPa pressure and more than 100°C water is no longer incompressible, and compression will always result in a temperature increase. We cannot use the simple incompressible liquid formula to determine pump work, however need to evaluate the various values of enthalpy from the Compressed Liquid Water tables, leading to the following results:
Notice that the isentropic compression of the liquid to 25 MPa resulted in a temperature increase of 3.6°C, thus the actual temperature rise of 5°C lead to a pump adiabatic efficiency of 82%. As an exercise, assuming that the liquid water behaves as an incompressible fluid, determine the pump efficiency for the given temperature rise from 170°C to 175°C [ηP = 55%]
Note: Recall from Problem 6.3 that in solving this exercise you will need to use the following relations for an incompressible fluid:
where CH2O = 4.18
kJ/kg.K and specific volume v = 0.001 m3/kg.
Thus
for the isentropic process: (Δs = 0) ⇒ T2
= T1 (ΔT
= 0).
__________________________________________________________
In the Gavin Power Plant, each generating system has a single-stage feedwater pump driven by a steam turbine, as shown below. Its purpose is to pump the condensed saturated-liquid water at 800 kPa, 170°C to a high pressure of 30 MPa at the inlet to the boiler. The pump is powered by a dedicated 48.49 MW (65,000 hp) turbine. On a recent visit to the Gavin Power Plant we were informed that the liquid water will normaly experience a temperature rise of around 5°C during this process. The inlet pressure to the steam generator is 30 MPa, however the water has to pass through 350 miles of piping and undergoes a 5 MPa pressure drop while being heated to 550°C, thus the inlet pressure to the high pressure turbine is 25 MPa.

__________________________________________________________________________________