Charged particles, such as electrons, ionized atoms, nuclei, etc., can have their kinetic energy increased by electric fields. This acceleration can be achieved in two ways: with a DC field created by applying a large potential difference between two electrodes (e.g., conventional X-ray and Van de Graf machines) or with multiple exposures to AC fields (e.g., cyclotrons and LINACs) craftily arranged so that each time the particle is exposed to the field it is in the right phase to increase the particle's energy.
During and after the acceleration the charged particles may be guided by electric or by magnetic fields (more often the latter). These guides may just serve to define the path followed by the particles, but usually will also serve to focus the beam: those particles that stray from the intended path will be brought back to it.
There are two major classes of particle accelerators, linear and curved. In both the cyclotron and synchrotron for example, the particles' paths are bent by magnetic fields and each time around the kinetic energy is increased slightly. A LINAC, on the other hand, contains many regions (microwave cavities) along the straight trajectory where acceleration occurs.
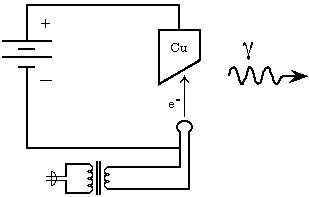
In conventional X-ray generators a metal anode is bombarded by high kinetic energy electrons, as shown in Fig. 1. "LINAC" X-ray generators (discussed further in Chapter VII) simply use a different technique to achieve high kinetic energy for the bombarding electrons. Synchrotron light sources, on the other hand, produce photons when fast electrons are subjected to alternating lateral forces during their continuing trajectory. When electrons in a conventional or LINAC generator strike the anode, roughly 99% of them experience nothing spectacular; they undergo sequential glancing collisions with particles of matter, lose their energy a little at a time and merely increase the average kinetic energy of the particles in the target; the target gets hot. Perhaps one percent of the incident electrons contribute a photon to the X-ray spectrum.

Figure 1: Schematic Diagram of an X-ray Generator. The heated filament boils off electrons, which then accelerate toward the positively charged Cu anode. The photons are absorbed by shielding and collimators (not shown), except those headed along the main beam axis. (After Piccard and Carter, 1989.)
Two mechanisms produce X-ray photons: first, the sudden deceleration of the electrons produces photons with a wide distribution of energies, ranging from very tiny up to the kinetic energy of the incident electrons. These photons (known as "bremsstrahlung," German for "braking radiation") have a continuous spectrum with a broad peak of intensity for photons with roughly half the incident electron energy, and are more numerous in directions perpendicular to the electrons' acceleration vector (see Feynman, Vol. I, ch. 28).
Roughly as many X-rays are generated by the second mechanism, which begins when an incoming electron "chips off" an inner electron from an atom of the anode. Following such an ionization event, an outer electron drops down to fill the vacancy, emitting a photon of energy equal to the difference between the binding energies of the old and new states of this (orbital) electron. Photons of this sort have energies that are, of course, characteristic of the anode material, and are emitted from the atom with equal probability in all directions. We thus expect the spectrum of a conventional X-ray generator to show a combination of continuous and line features.
Characteristic X-ray photons are typically energetic, because with sufficiently energetic incident electrons, the ionized electrons are most frequently removed from the K or L shells. This can be understood qualitatively on the basis of quantum mechanical perturbation theory for incident photons. (Viewing the Coulomb interaction between the incident electron and the atomic electron as mediated by virtual photons motivates this approach.) Perturbation theory provides the dual result that, first, the probability of ejecting the atomic electron is zero, if the incident particle's energy is less than the binding energy of the electron, and, second, that the probability for the case of a photon incident upon an atom is inversely proportional to the square of the excess energy, if there is enough (see, textbook discussions of perturbation theory, for example, in Dicke and Wittke, Messiah, or Davydov). Therefore, the probability of ejecting an outer shell electron is small, since it will have a much larger excess energy (see Marmier and Sheldon); this conclusion holds for incident electrons or photons.
One way to visualize the origin of the bremsstrahlung radiation is to consider the electric field lines surrounding an electrically charged object: if it is stationary, they will spread out radially; the increased separation at greater distances corresponds directly to the inverse-square reduction in field strength. If a charge is moving steadily at a speed << c, then the reasonable picture is just that the field lines move with the object. If the speed approaches c, then we need to know that actually the electric field at any distance will depend upon the location of the charge not at the present time, but rather at an earlier time,
![]()
where r is the distance from the charge's location at tr to the point of observation, and tr is known as the "retarded time" (see Feynman, Vol. I, ch. 28, which discusses the largest term in the electric field, the electromagnetic radiation). The exact solution requires a Lorentz transformation of the electromagnetic field tensor, but qualitatively, motion produces a curvature to the field lines; any sudden change in velocity will therefore require the field lines to change their curvature. This leads us to think of the bremsstrahlung as "cracking the whip in the electric field lines," creating a wave of electromagnetic radiation. (This analogy is often attributed to Maxwell.)
As discussed by Jackson (1987), Evan Jones Williams analyzed bremsstrahlung relativistically from a frame at rest with respect to the initial motion of the electron. In this view an electron at rest is bombarded by a nucleus. The Coulomb field of the nucleus is viewed as composed of a multitude of "virtual photons," which may Thomson scatter or Compton scatter off of the electron (see chapter IV, section B). Detailed analysis does produce predictions equivalent to those of the conventional analysis in the laboratory frame discussed above.
The bremsstrahlung spectrum is continuous, the minimum wavelength (maximum photon energy) being determined by the accelerating voltage (in the case of a conventional tube): by conservation of energy, the photon energy cannot exceed the pre-impact kinetic energy of the electrons bombarding the anode. The characteristic photon energies cannot exceed the difference between the state energies of the K shell and the valence shell, and the most energetic of the commonly observed characteristic photons, the ![]() , have roughly 90% of that energy. The most energetic characteristic photons will only be observed if the bombarding electrons had enough energy to eject K shell electrons, hence the bremsstrahlung limit will always be more energetic than the most energetic observed characteristic photon. In describing the spectrum of x-radiation, one should specify the Bremsstrahlung end-point and the composition of the anode (to identify the characteristic lines). For conventional medical X-ray tubes, however, the usual style is to specify simply the maximum, or peak, accelerating potential, using units of "kVp." The value will be the same as the energy of the most energetic photon present, measured in keV. If the accelerating potential is obtained from a conventional AC power source, then instead of being a constant value, it will be a unipolar but fluctuating value, and an even higher fraction of the photons will have substantially less than the peak energy: at each instant, the peak photon energy is determined by the accelerating potential at that instant.
, have roughly 90% of that energy. The most energetic characteristic photons will only be observed if the bombarding electrons had enough energy to eject K shell electrons, hence the bremsstrahlung limit will always be more energetic than the most energetic observed characteristic photon. In describing the spectrum of x-radiation, one should specify the Bremsstrahlung end-point and the composition of the anode (to identify the characteristic lines). For conventional medical X-ray tubes, however, the usual style is to specify simply the maximum, or peak, accelerating potential, using units of "kVp." The value will be the same as the energy of the most energetic photon present, measured in keV. If the accelerating potential is obtained from a conventional AC power source, then instead of being a constant value, it will be a unipolar but fluctuating value, and an even higher fraction of the photons will have substantially less than the peak energy: at each instant, the peak photon energy is determined by the accelerating potential at that instant.
The bevel on the anode surface as shown in Fig. 1 is typical. The angle is a compromise between two competing goals. First, it permits a small apparent source diameter when the beam is collimated, while permitting the electrons to land on a larger area of the anode. This spreads out the heat that they deposit, permitting higher power operation without melting the anode. This feature is optimized with a small, but non-zero, angle between the beam direction and the anode surface. (Zero degrees would result in excessive absorption of photons emitted from slightly inside the anode surface, because they would have to travel a longer distance through the anode in order to emerge heading for the collimator.) Second, the bevel permits selection to emphasize the bremstrahlung or the characteristic spectrum, because the characteristic spectrum will be isotropic, but the bremsstrahlung will be most intense perpendicular to the acceleration vector of the stopping electrons, so the characteristic spectrum will be emphasized with a large angle between the beam direction and the anode surface.
In short then, the electron beam current in the X-ray tube determines the overall intensity of the spectrum. The accelerating potential of the tube determines the shape and end point of the continuous spectrum. The composition of the anode (pure copper, copper-silver alloy, etc.) determines the wavelengths present in the line spectrum. The angle between the beam direction and the anode surface determines the balance between the line and continuous spectrum and the effective size of the source. To test this explanation of the continuous spectrum, we follow Einstein's argument, that emission and absorption of electromagnetic energy are both "quantized," and apply Planck's formula from the explanation of the photoelectric effect:
![]()
where ![]() is the energy of each quantum, h is Planck's constant, and f is the frequency of the electromagnetic wave.
is the energy of each quantum, h is Planck's constant, and f is the frequency of the electromagnetic wave.
Since f ![]() = c, where c is the speed of light, and since conservation of energy prohibits the radiated energy exceeding the pre-impact kinetic energy of the incident electron, we must have that
= c, where c is the speed of light, and since conservation of energy prohibits the radiated energy exceeding the pre-impact kinetic energy of the incident electron, we must have that ![]() , where V is the accelerating potential and e is the electron's charge. Therefore, we find that
, where V is the accelerating potential and e is the electron's charge. Therefore, we find that
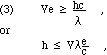
Since Eq. 3 is an inequality, an experimental observation of the shortest wavelength present will establish a limit on the value of Planck's constant, h. In a diffraction experiment, this will require the evaluation of the scattering angle for the "end point of the spectrum," the small angle (high photon energy) for which the observed intensity falls to zero.
When atoms undergo quantum transitions to states of lower final energy, they routinely emit electromagnetic radiation characteristic of the element, with photon energy equal to the difference between the initial and final state energies. The atomic states with higher principle quantum numbers (the N, O, P, and Q levels) are closely spaced in energy, and hence the photons emitted for transitions among them are of small energy and long wavelength, often infrared or visible light. The initial states with low principle quantum numbers (the K, L, and M levels) are more widely spaced in energy, and hence the photons emitted for transitions among them (or from the higher states to them) are of large energy and short wavelength, typically ultraviolet or X-rays. If the consequence of impact by a bombarding electron is the ejection of a target atomic electron, the remaining "atomic core" is an ionized atom, which will usually be in a highly excited state, since typically an inner-shell electron will have been ejected. This ion will relax to its ground state and then probably capture a valence electron from a neighbor. The relaxation to the ground state usually is achieved by a cascade of single- or double-level jumps by electrons from occupied states in higher levels "falling into" the "holes" in the lower energy levels. As just described, the photons released during these jumps will range from X-rays to visible or infrared light.
The least energetic radiation in the K-series is the ![]() , which is emitted by transitions from the L level to the K level. More energetic is the
, which is emitted by transitions from the L level to the K level. More energetic is the ![]() , which is emitted by transitions from the M level to the K level. (The L level is a mixture of states having slightly differing energies, so that
, which is emitted by transitions from the M level to the K level. (The L level is a mixture of states having slightly differing energies, so that ![]() radiation has a "fine structure," e.g., includes several very close wavelengths.) Because the
radiation has a "fine structure," e.g., includes several very close wavelengths.) Because the ![]() photons are more energetic than the
photons are more energetic than the ![]() photons, the wavelength of the
photons, the wavelength of the ![]() radiation is shorter than the
radiation is shorter than the ![]() . But the wavefunctions of the electrons in the L level overlap more with those for the K level, than do the wavefunctions of the electrons in the M level, so there is a greater transition probability for L to K than for M to K. Therefore we observe a greater "population" of
. But the wavefunctions of the electrons in the L level overlap more with those for the K level, than do the wavefunctions of the electrons in the M level, so there is a greater transition probability for L to K than for M to K. Therefore we observe a greater "population" of ![]() photons than of
photons than of ![]() photons in the X-ray beam.
photons in the X-ray beam.
The minimum pre-impact kinetic energy of the electron beam that is needed to eject a K shell electron can be estimated fairly well using the extended Bohr model for the energies ![]() of the states of a single electron bound to a nucleus of charge Z:
of the states of a single electron bound to a nucleus of charge Z:
![]()
where n=1 is the ground state, n=2 is the first excited state, and so on. (The numerical value stated above is subject to small corrections for the fact that nuclear mass is not infinite.)
Equation 4 can be used, with less precision, to estimate the ![]() or
or ![]() photon energies for atoms that have had a single K-shell electron ejected. Within this approximation, the
photon energies for atoms that have had a single K-shell electron ejected. Within this approximation, the ![]() photons will have energy equal to
photons will have energy equal to ![]() , and the
, and the ![]() photons will have energy equal to
photons will have energy equal to ![]() . Thus, if the electron beam has sufficient energy to eject K shell electrons, producing
. Thus, if the electron beam has sufficient energy to eject K shell electrons, producing ![]() and
and ![]() radiation, it will have enough energy to produce some bremsstrahlung photons with even more energy, as previously mentioned.
radiation, it will have enough energy to produce some bremsstrahlung photons with even more energy, as previously mentioned.
The short wavelength limit of the continuous "white" spectrum is dependent uniquely on the kinetic energy given to the electrons by the potential difference between the anode and the electron-emitting filament, regardless of the anode's material; the "characteristic" line spectrum, superimposed upon the white spectrum is due to the elemental composition of the anode and the energy-levels associated with that specific atomic electron system. Measuring the intensity as a function of wavelength for the photons in an X-ray beam (typically done by crystal diffraction, as will be discussed in Ch. VIII) permits determination of
The processes of X-ray emission, as described above, are such that the wavelength range produced can overlap both the ultra-violet, on the low energy end, and the gamma on the high energy end of the electromagnetic spectrum, depending on the accelerating potential and the anode material. The name used to describe a radiation with high photon energy (an ionizing radiation) is conventionally chosen on the basis of its source, rather than its wavelength. "Ultra-violet" or "fluorescent" radiation follows after atomic electron ionization or excitation by photon absorption, and "Gamma" radiation is emitted by nuclei in conjunction with radioactive disintegration or the relaxation of nuclear excitations, while "X-rays" follow atomic electron ionization by impact of bombarding electrons, or in the relaxation following nuclear decay.
Neutrons are radiated copiously (and energetically!) from nuclear fission reactors and weapons. They can also be produced in more reasonable circumstances. If an energetic alpha particle strikes a Be-9 nucleus (the common isotope), there is a significant probability of forming an intermediate nucleus that is an excited state of C-13, that then decays to C-12 plus a neutron, as shown in Eq. 5, below. The asterisk indicates an energetic, transitory, intermediate nuclear state, much as a chemist might write an intermediate compound in square brackets.
![]()
The energy of such a neutron varies widely, roughly from 0.5 to 11 MeV, with a peak in the neighborhood of the initial alpha energy.
A common source of suitably energetic alphas is the decay of a heavy element such as plutonium. Plutonium and beryllium will form a solid solution alloy if they are melted after mixing in the proper stoichiometric ratio. Because of the radiation and chemical hazards presented by those two metals, especially in powder form, many such solid sources have been made. They are enclosed in stainless steel holders welded shut around an inner welded steel container. They are filled in powder form, welded shut, and then melted to form the alloy by using heat from electromagnetic induction.
Because many of the alpha particles simply slow down without nuclear interaction, the interior of the container gradually fills up with helium atoms. These atoms will accumulate until all of the plutonium has decayed. The pressure achieved can be directly calculated from the gas laws: it is clearly necessary to allow "empty space" inside that will keep the ultimate pressure within bounds. The situation is perhaps not that bad, since the inert helium atoms can diffuse through the steel walls of the container, but that diffusion is very slow, so proper allowance must be made.
These energetic neutrons can be used directly or after slowing down to "thermal" energies (< 1 eV). The use of neutrons to "activate" stable nuclei, as discussed in chapter IV, usually involves such thermal neutrons. The interactions between neutrons and matter is essentially between neutrons and nuclei. Such collisions transfer significant energy from the neutron only if the nucleus has a mass comparable to the neutron's 1 amu. Thus, "moderators" of neutron energy are typically water or hydrocarbons that contain many hydrogen atoms.
A variety of secondary radiation can be generated by the interaction of ionizing radiation with target materials. As discussed in Chapter IV, atomic electrons can be ejected by collisions with the incoming radiation. If the sample contains hydrogen atoms it is also possible that you may observe ejected protons (this is much more likely with neutrons or alphas than with betas or gammas incident).
If neutrons or alphas are incident with appropriate energies, they can undergo nuclear reactions with the target. Sometimes the resulting nucleus will be stable, but often it will be radioactive itself. Another possible outcome of high energy nuclear particle (proton, neutron, or alpha) bombardment is the creation from that kinetic energy of new material particles. These can include charged particles, such as electrons, positrons, and muons, that are also created by high energy beta and gamma radiation. Nuclear particle impacts are particularly likely to create other nuclear particles, though, of which the easiest to create are pions, because they have the smallest mass. One point to keep in mind is that muons, pions, neutrons, and most of the more exotic types are radioactive, leading to further ionizing radiation. Usually the particles are created in pairs, one normal and one anti-particle. If it does not first decay in flight, the anti-particle may, after stopping, annihilate with an existing normal particle from the target. This typically produces a pair of high energy photons headed in opposite directions. See the discussion at the end of section C of chapter IV.
Dick Piccard revised this file (https://people.ohio.edu/piccard/radnotes/artificial.html) on December 4, 2003.
Please E-mail comments or suggestions to piccard@ohio.edu.