Figure 1: (a) Histogram (b) Distribution
Scientific experiments, whether instructional exercises or original research, routinely involve the measurement of multiple quantities. Typically, some of those quantities are controlled by the experimenter (the "causes" or "independent variables") while others are simply observed (the "effects" or "dependent variables"). In many situations, the connections among the directly measured quantities are most readily understood by comparing values that can be calculated from them. For example, you would expect the power delivered by a single-cylinder gasoline engine to be closely related to the displacement volume of the cylinder, but you may have directly measured only the diameter and stroke length. When we use mathematics to infer a quantity from direct measurements of other quantities, we often describe the result as an "indirect measurement."
The heart of any measurement process is deciding whether the quantity being measured is greater than, equal to, or less than some reference value. The simplest type of measurement involves the direct physical comparison of a standard to the unknown quantity (e.g., measuring the length of an object with a ruler, or the temperature with a conventional mercury thermometer). Such "analog" measurements provide the experimenter with an immediate, intuitive feel for their uncertainty, because the experimenter must directly judge the comparison between the object and the standard. The markings on the scale will have some non-zero width, the object may not have well-defined boundaries (where is the edge of a cotton ball, anyway?), and, depending on the spacing between the finest markings on the scale and the visual aquity of the experimenter, it may well be possible to honestly estimate more precisely than the scale is marked (although rarely more precisely than to the tenth of the finest markings).
The raw data of an experiment are sometimes digital in nature: counted radioactive decays, response bar pressings by a rat, etc. In such cases, provided that the apparatus functions properly, there will be no doubt about the number observed for a specific experiment (although, as we will discuss below, a different number might be observed if the experiment were repeated). Often, however, the data are analog signals, such as the temperature, which is converted by some suitable transducer into a voltage or current proportional to the physical quantity being measured, and then converted by an electronic analog-to-digital-converter ("ADC") into a number that measures the electrical quantity in some suitable units. This may be done with custom electronics or with a commercial digital meter. In either case, the uncertainty in the result is less likely to be intuitively obvious to the experimenter than the uncertainly of an analog measurement. We expand on this topic in section H.
Laboratory work provides more than just practical experience working with the equipment. Critical in the education of a scientist is the development of an understanding of the limitations of experimental results. The first stage of this error analysis is the identification of sources of errors in measured quantities, and their relative impact on the possible conclusions. The second stage is using the "rules of thumb" for significant figures. (It is wise to carry at least one extra figure through all intermediate calculations, rounding-off to the correct number of significant figures only at the end. This practice of using a "guard digit" reduces the compounding of round-off errors with the unavoidable experimental fluctuations, and in this day of cheap calculators adds little to the work or to the likelihood of mistakes.) In the third stage of error analysis, more exact propagation of error estimates is made in calculations, notebooks, and written lab reports, and the reports indicate first, what specific steps, not part of the original statement of the experiment, were taken to reduce the impact of the major sources of error, and second, suggest additional steps for others to use.
The focus of this chapter is basic statistical error analysis, the methods used to analyze data and to communicate honestly the quality of experimental results. The estimation of systematic errors can be refined with the aid of statistical techniques, but it remains a subject calling for educated judgement. The mathematical and philosophical rationale for some of the methods is discussed. No attempt is made to familiarize the student with particular computer routines for performing the calculations.
The references cited throughout this chapter are given in full in the Bibliography.
The crux of modern science is the reproducible experiment. By this we do not mean that the numerical results would be exactly the same every time, if the experiment were repeated, but rather that the variations would be consistent with the idea of random (statistical) errors. Thus, repeated measurements of the same quantity mostly yield results close to the "true value," and only rarely yield results that are very different. Random errors must be distinguished from sheer mistakes and from systematic errors. There are two possible origins of random errors: the unavoidable variations in judging instrumental readings while measuring a well-defined quantity, and "variations that arise from chance associated with the sampling of a (non-uniform) population or of any random variable" (Rajnak, 1976). The word "error" has three primary meanings in the present context: first, the deviation of an individual measurement from the "true value," second, the uncertainty of a result, and third, the discrepancy between a result and the "true value." Usually we will intend the second meaning, but do be alert to judge from context which of the three is intended.
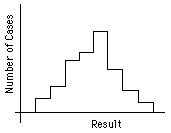
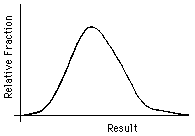
One way of presenting the results of a series of measurements is the "histogram," or "spectrum": the range of possible results is split evenly into intervals; the result of each measurement is tallied to the interval containing it; finally, the tally is graphed, as shown in Fig. 1a. The "distribution curve" for an experiment is the continuous curve that we expect as the limiting histogram when more and more measurements are taken and the results are shown tallied and graphed in smaller and smaller intervals; see Fig. 1b.
Many measurements yield distribution curves that are smooth, single-peaked, and symmetrical. Sometimes the curve is fairly accurately described by the standard bell-shaped curve, the "Gaussian" or "normal" distribution. Often, however, the distribution curve that describes the results will have a more complicated form. Any experiment that involves counting radioactive decays, for example, will have a distribution curve that is not symmetrical, since there is a smallest number of counts that can be observed in any given period of time: zero! (See Appendix D.) The process of digitizing an analog signal (see section H) involves rounding-off, which exhibits a flat-topped distribution, one of the few such in experimental science.


Figure 1: (a) Histogram (b) Distribution
If the distribution curve is symmetrical we have no problem agreeing that the true value for the measurement is the central value. On the other hand, it is not so obvious how to identify the true value for an asymmetrical distribution. The three common "measures of central tendency" are the mode (Fig. 2a), the median (Fig. 2b), and the expectation value (Fig. 2c). The mode is the most likely result, namely that value for which the distribution curve is at its peak. The median is the value that splits the area under the distribution curve equally. (It is an even chance whether any given result will be above or below the median.) The expected value is just the limit (as the number of measurements increases to infinity) of the average value, defined in the usual way as the sum of the results divided by their number; in other words the expectation is the "population mean." We ordinarily regard the expectation value as the best indication of "central tendency" for a distribution, and will therefore be interested in the average of the measurements actually made.
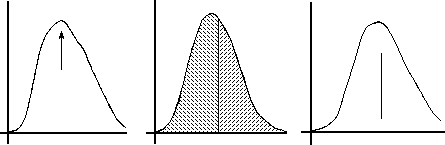
(a) Mode (b) Median (c) Expectation
Figure 2: Which is the true value?
The "precision" of a measurement is essentially the width of the peak in the distribution curve, and the "relative precision," where that idea is used, corresponds to the width of the curve divided by the true value (often expressed as a percentage). There are several ways to describe mathematically the width of the curve: the "full width at half maximum" (Fig. 3a), the "probable error" (Fig. 3b), and the "standard deviation" (Fig. 3c) are three very common methods. Each of the width parameters is defined using the distribution curve, which describes an infinite number of measurements. The probable error may be defined as half of the narrowest full width that encompasses half the area under the distribution, as shown by the speckled area in the central part of Fig. 3(b). This will be found as a region with end points at which the distribution is equally high.
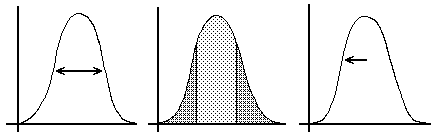
(a) F.W.H.M. (b) P.E. (c) S.D.
Figure 3: Parameters for Distribution Width
The definition of the distribution (or "population") standard deviation, ![]() , (sigma) is "the square root of the average value of the squares of the deviations of the data from the true value," as shown in Eq. 1:
, (sigma) is "the square root of the average value of the squares of the deviations of the data from the true value," as shown in Eq. 1:
![]()
This is the distribution's root mean square (rms) deviation. In some cases you will be interested in the rms deviation of your data set, and in other cases you will want to estimate the distribution standard deviation, based on your data. Although the FWHM and the PE are always reasonable, there are experimental situations in which the true distribution curve gives an infinite value for the standard deviation!
Typical experimental situations involve so few measurements that the distribution curve is only roughly suggested. When analyzing experimental data, therefore, you can determine only estimates for the expectation value or any of the width parameters. The usual practice is to quote the result of the measurements as a single number, the "best estimate of the true value," and to give some indication of the width of the distribution. The two common formats are to specify a tolerance and to specify upper and lower limits for the true value. For example:
or equivalently,
Suppose an experiment has been performed a few times, and the true value and the width of the distribution curve are to be estimated. If it is no worse to err on one side or on the other, one is "unbiased" and should report the following: first, the best estimate of the true value is the "mean," or average of the data:
![]()
Second, the best estimate of the distribution standard deviation is the "standard error" of the data:
![]()
Using N-1 and the mean in Eq. 3, instead of N and the true value as in Eq. 1, partly offset each other, which is why Eq. 3 gives a good estimate for the standard deviation. Observe that s will always be less than half of the "range" of the observed values, the difference between the highest and lowest values.
Equations 4, below, present an alternative way to calculate the standard error, which we will use in deriving Eq. 13, in section D, below. It should be evident that Eq. 4b is simply an abbreviated form:
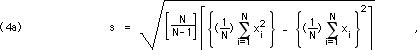
or
![]()
Proving the equivalence of Eqs. 3 and 4 requires about half a page of algebra, which we will not indulge in here. The second factor in square brackets on the right side of Eq. 4 may be verbalized as "the average of the squares of the data values minus the square of the average value of the data." Equation 4 is the method used by those hand calculators that can determine mean and standard error.
Because of the subtraction of two nearly equal numbers in Eq. 4, all intermediate steps must be carried out with many extra significant figures to get accurate final results for s. Therefore, hand calculation or simple computer programs should definitely take the approach of Eq. 3, to reduce the impact of round-off error, unless you can use at least ten significant figures. Use "double precision" arithmetic in computer programs: in most computer systems, ordinary BASIC, FORTRAN, and PASCAL calculations are rounded off to six or seven significant figures at every step.
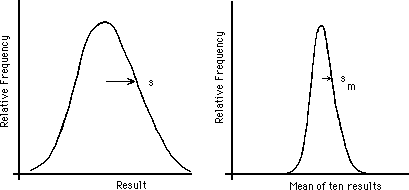
Figure 4: (a) Measurement Distribution (b) Mean Distribution
If one considers a single measurement as an estimate of the true value, then the uncertainty in that estimation is the distribution standard deviation, ![]() . If one has made only the single measurement, an estimate, s, of
. If one has made only the single measurement, an estimate, s, of ![]() cannot be determined by Eq. 3; one must proceed intuitively (or, in the case of a Poisson distribution, use Eq. D-3). With several measurements we report the mean value as the best estimate of the true value, as discussed above. But how close to the true value can we expect the mean to be? That is, suppose that one takes the same number of measurements all over again; how close should the new average be to the old one? If the errors in the measurements are random and independent, with no systematic effects or correlations between measurements, then the width of the distribution curve for the means is related to the width of the distribution curve for the measurement and to the number of values averaged:
cannot be determined by Eq. 3; one must proceed intuitively (or, in the case of a Poisson distribution, use Eq. D-3). With several measurements we report the mean value as the best estimate of the true value, as discussed above. But how close to the true value can we expect the mean to be? That is, suppose that one takes the same number of measurements all over again; how close should the new average be to the old one? If the errors in the measurements are random and independent, with no systematic effects or correlations between measurements, then the width of the distribution curve for the means is related to the width of the distribution curve for the measurement and to the number of values averaged:
![]()
where sm, the "standard error of the mean," is the best estimate of the uncertainty in estimating the true value by using the mean of N measurements (see Fig. 4). There is a convention that "standard deviation" refers to the r.m.s. deviation of a distribution curve, whether for the data or for the means, and "standard error" refers to an estimate of the corresponding standard deviation, based on a (limited) set of data.
The estimates s and sm are themselves subject to variation, especially when N is small. Even for N as large as ten there will typically be 25% fluctuations in the value of s, or sm, as evaluated from successive samples; see section D, below, especially the discussion of Eq. 9. It is therefore practically never sensible to quote more than one or at most two significant figures for s or sm. The estimated true value should be quoted to the same number of decimal places as the error, however many significant figures that gives. For example, if one has computed
and
then the asserted result should be
It is usually much easier to grasp the significance of the data "at a glance" when it is presented this way, with both the power of ten and the units "factored out."
Sometimes you will be tempted to discard an observation that seems to be a mistake, rather than include it with the rest of your data and be forced to report a large value for s. If there is an obvious reason, such as being off by one in the most significant digit, such rejection of data may be justified. Generally, extreme caution should be exercised. A rule of thumb, depending on the number of measurements, is that data within three distribution standard deviations from the mean should be kept. (That leaves it up to your judgment whether the mean and standard error used to decide upon rejection should be calculated with or without the questionable data.) Report (at least in a footnote) the fact that data have been rejected, and also the mean and standard error that would have been obtained without rejection, unless there is a clear physical basis for discarding the data; inconsistency with other results, although unfortunate, is not "physical."
Whenever a result can be compared to an "accepted value," further calculations are evoked. A common but by itself not very informative one is the "per-cent error": the discrepancy, the difference between the result and the accepted value, expressed as a percentage of the accepted value. A much more useful statistic is the "t-score," the discrepancy between the accepted value and your experimental result, measured in terms of the uncertainty of your experimental result, calculated as follows:
![]()
where sexpt will typically be a standard error of the mean.
Table I: T-score ProbabilitiesBased on Gaussian errors with the experimental | |
| Possible Value of |t| | Probability that |t| calculated from data exceeds |t| value listed in first column. |
| 0.2 | 0.84 |
| 0.4 | 0.69 |
| 0.6 | 0.55 |
| 0.8 | 0.42 |
| 1.0 | 0.32 |
| 1.5 | 0.15 |
| 2.0 | 0.045 |
| 2.5 | 0.014 |
| 3.0 | 0.0027 |
| 3.5 | 0.0005 |
An alternative form is used to calculate t when the issue is the significance of the discrepancy between two measured results:
![]()
where we are now dividing the discrepancy by the uncertainty in the discrepancy, as calculated based on Eqs. 13, 14, and 18, below.
As shown in Table I, it is common to find the absolute value of t less than 1.0, and very rare to find it larger than 3 unless something is wrong. The larger the absolute value of t is, the more suspect the experimental procedure, the calculation method, or the arithmetic itself, although it is definitely true that once in a while pure chance will produce a large t even with no systematic errors or mistakes. Table I displays the probability of obtaining various values of t for a particular case. (This is a reasonable guide even for many other cases.) The value of t will have at most two significant figures, because it is calculated from the experimental s (see the discussion of Eq. 9, below).
The measurements made in the laboratory are often not the quantity of interest, but rather are used to calculate a result (an "indirect measurement"). We discuss here the methods used to estimate uncertainties in such calculated results, based on the uncertainties in the measured quantities. Our discussion will involve two approaches: first, the "rules of thumb" for significant figures, and second, the more precise finite differences method.
The number of significant figures in a directly measured quantity is determined by writing that quantity rounded off to the last digit that you know something about. That is, the uncertainty in the last digit presented should be between 1 and 9. The number of significant digits is then just the number of digits that are needed when the number is written in scientific notation. For example, if 26,423 is the measured value, with an uncertainty of 35, then it should be rounded off to 26,420 which would be 2.642 * 104 in scientific notation. Hence, we say that this value is known to four significant figures. Using this definition of significant figures, the rules for establishing the number of significant figures in the results of arithmetic operations performed on measured values can be summarized according to the type of calculation:
The 3.267 has four significant figures and the 4.93 has 3 significant figures; therefore, the calculation should be written as shown below. Observe that the answer has fewer significant figures than some of the entering values.
When the first significant digit of the answer is a 1 or a 2, and at the same time the entering value whose number of significant figures was fewest has a first significant digit of more than 3, as in this case, one may be justified in keeping one extra significant figure, reporting here, for example:
The hundredths figure is the last significant figure of 111.45 and the thousandths figure is the last significant figure of the other two numbers. Therefore the answer should be rounded off to the hundredths:
Finally, express the result in normal scientific notation:
Observe that the number whose value provided the limitation on the significant digits was not the number that itself had the fewest significant digits. Furthermore, this gives five significant figures in the answer, even though one of the original numbers had only two:
Now we examine "the truth behind significant figures." We first discuss the simpler case, in which only one measured number enters into the calculation and then we discuss the more complex case, in which several measured numbers are used. We consider cases in which one physical quantity, say x, is directly measured, giving a best estimate <x> (typically the mean of several trials), with uncertainty sx (typically the standard error of the mean of those trials), and in which what we want to know is a value, say f(x), that can be calculated from the measured quantity on the basis of some theory. (As usual in discussions dealing with the random errors of measurement, we restrict ourselves to those cases in which there are no systematic errors in x, so that the mean value of x is the best estimate of its true value.) For example, we might measure the diameter, d, of a bar, giving a best estimate <d>, with uncertainty sd, but want to know the cross sectional area,
A sensible procedure in such simple cases is to perform the calculation two times: once with the best estimate of the data value and once with the upper or lower limit. (This last may be called calculating with "deviated data.") First we calculate
(7) f0 = f(<x>) and f1 = f(<x> + sx ) .
The best estimate for f is clearly f0; an estimate for sf, the uncertainty in the value of f, can be calculated readily by subtraction:
(8) sf = |f1 - f0 | .
As discussed below, the degree of confidence that applies to sf is the same as that which applied to sx; for example, if sx is a good estimate of the standard deviation of x, then sf is a good estimate of the standard deviation of f(x).
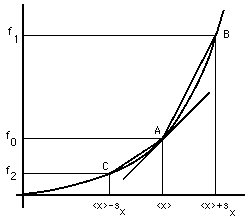
Figure 5. Propagating uncertainty for a function of a single measured quantity. The point A is (<x>,f0); B is (<x>+sx,f1); and C is (<x>-sx,f2). The extended line is tangent at the point A. The chord to the right, from A to B, has slope mR; the chord to the left, from A to C, has slope mL.
Consider Fig. 5, whose shape is appropriate to our example of the cross section area of a bar of measured diameter. The significance of Eq. (8)'s difference in function values is immediately evident, but what are the limitations of the approximation? In particular, consider the asymmetry of the results obtained by subtracting sx, instead of adding it, in Eq. (7)'s calculation of f1, obtaining instead the value f2.
Equation (8) may be restated in terms of the slope mR of the chord to the right (from point A to point B in Fig. 5), giving the same value for the uncertainty as above:
(8a) sf = (mR) * (sx) .
Using f2 instead of f1 in Eq. (8) is equivalent to using mL, the slope of the chord to the left (from point A to point C in Fig. 5), giving a value for the uncertainty that will in general be different:
(8b) sfb = (mL) * (sx) .
One could use a truncated Taylor's series for f to approximate either Eq. (8a) or Eq. (8b), using the slope of the line tangent at point A, giving a third value for the uncertainty:
(8c) sfc = (df/dx) * (sx) .
For example, in our case of determining the cross sectional area of a rod, we obtain the following from Eq. (8c):
This is intuitively reasonable in terms of the radius r, since sr = sd/2, and ![]() <d>sr is the area of a circumferential strip of radial width sr.
<d>sr is the area of a circumferential strip of radial width sr.
Although the three variant forms of Eq. (8) are identical in the limit of small uncertainties, they do not in general produce identical results with non-zero values for sx. (In terms of the three forms of Eq. (8), we do not expect that sf = sfb = sfc.) It is not obvious which variation of Eq. (8) provides the best estimate of the uncertainty in our derived result. Whatever the probability that the true value of x is between <x> - sx and <x> + sx, the probability must be the same that the true value of f is between f2 and f1. This intuitive assertion for the single variable case does not hold true in general for the multi-variable case we will consider later (Silverman and Strange, 2004).
What is the most appropriate terminology for describing asymmetrical error limits? Because of the uncertainty of sx itself, it is usually both unreasonable to specify separate high and low limits, and immaterial which variation of Eq. (8) is used. Mendenhall (1983) addresses the uncertainty of the standard error in terms of the chi-squared distribution for s as an estimate of ![]() . Higbie (1976) demonstrates that in the limit of large N, the standard error of the mean is
. Higbie (1976) demonstrates that in the limit of large N, the standard error of the mean is ![]() times the uncertainty of the standard error itself. Hence, if we follow Higbie and denote the uncertainty of the standard error, s, by SD(s), and the uncertainty of the standard error of the mean, sm, by SD(sm), as calculated from N observations, then we can approximate them by
times the uncertainty of the standard error itself. Hence, if we follow Higbie and denote the uncertainty of the standard error, s, by SD(s), and the uncertainty of the standard error of the mean, sm, by SD(sm), as calculated from N observations, then we can approximate them by
![]()
and
![]()
Higbie shows by direct calculation that N need not be very large for Eq. (9) to be useful: for N=2, the estimate of SD(s) calculated from Eq. (9) is within 15% of the best estimate of SD(s), and for N=10 it is within 2%. Equation (9) implies that only experiments with N > 50 can claim to have determined sm or s to within ±10%. Therefore, for most instructional experiments, one need only specify a single value for the uncertainty, and any form of Eq. (8) provides a sufficiently accurate estimate for sf. For wildly bent functions, or very imprecise techniques, upper and lower limits may need to be calculated in parallel, and specified separately.
How should one estimate the uncertainty of a result calculated from measurements of several different quantities? The method of Eqs. (7) and (8) can often be used sensibly if one number entering the calculation, say x, has considerably fewer significant figures than the other numbers; all quantities other than x can then be regarded as exact for the purpose of the error estimates. In many cases, however, more than one of the measured quantities has comparable precision.
For the general case of two measured quantities, say x and y, we write the result as a function f(x,y). For example, we might measure the length and diameter of a bar and want to know its volume
However, before treating such cases as the volume of a cylindrical bar, we will examine the simplest multi-variable case: a calculated quantity that is just the sum of two measured quantities, f(x,y) = x + y. In this case we will derive by algebra the relation between sx, sy, and sf.
One potential difficulty must be considered: the possibility of interaction between the supposedly random errors in each measurement of x and y. In other words, will the error in measuring x be related to the error in measuring y? If there is any systematic correlation between the errors in x and in y, then we say that the errors "depend" on each other, otherwise we say that the errors are "independent." We will see that the algebra for the specific case of f(x,y) = x+y leads us directly through this difficulty.
We start with a commonly used form for the best estimate, s, of the standard deviation, based on Eq. 4, which applies to x and to y directly. We then apply it also to the quantity (x+y):
![]()
![]()
![]()
where the bar over a quantity denotes its mean value. For finite data sets we can apply the distributive, commutative, and associative laws as we square out the binomials of Eq. (11), and reorder the terms to obtain the following:
![]()
The first two expressions in the right hand square brackets of Eq. (12) are clearly the squares of sx and sy, respectively, but what is the significance of the third group? As shown by Bevington (1969, p. 121), it is the numerator of the standard statistical formula for the "correlation coefficient" between the two variables. If the errors in measuring x and y are independent, then the correlation between them is zero, and we have the following conclusion:
![]()
The estimate for sx+y provided by Eq. (13) will be too large if errors in measuring x are associated with offsetting errors in measuring y; similarly, the actual uncertainty will be larger than the estimate if the errors in x and in y reinforce each other.
Now we consider more general cases, where the functional relation between the measured quantities and the final result is more complicated than addition. We make no special assumptions about the function f(x,y). If we make single measurements of each quantity, x1 and y1, then we can say only that we expect the true result for f to be "somewhere near" to f(x1,y1). If we measure x and y repeatedly, continuing until we have obtained many pairs of data, it becomes possible to speak quantitatively about the random errors. Statistical analysis does not permit statements about the systematic errors, but does permit, through such techniques as those discussed here, the propagation of a systematic error, estimated on other grounds, through to a consequent uncertainty in the final result.
A simple, direct approach is to calculate a result from each pair of observations, and then to calculate the mean, standard error, and standard error of the mean of that set of results. There are two difficulties with this approach, one practical and one conceptual. The practical difficulty is that one often will not have equal numbers of observations of the various quantities entering into the calculation. It will rarely be a sensible allocation of experimental time to make equally many measurements of the various quantities. The experimenter's time should be spent reducing the uncertainty of the quantity that contributes the most to the uncertainty of the interesting result.
An alternative direct method is to calculate f(xi,yj), using every combination of one measurement of x with one of y, and from that set of values of f to calculate a mean and standard error of the mean. This method is reportedly enjoying some popularity among statisticians presently. It does not require equally many observations of each quantity, but it obviously requires computation galore, and with the limits on the accuracy of any uncertainty estimate, as shown by Eq. (9), that effort is not likely to be justified. Furthermore, it does not naturally generate estimates of the contributions to the uncertainty from each source, so that there is no guidance offered to the experimenter as to how to allocate his or her time for additional measurements or improvements to the apparatus. (An interesting alternate technique is presented by Kinsella, 1986.) One could re-run the calculations using all the various measured values for all but one of the variables, and using only the mean value of that one. The reduction in the calculated standard error would then be attributed to the uncertainty of the one variable. This is even more hideously computation-intensive, though, so it would rarely be of any practical use.
We have seen the practical difficulties with the single-step approaches. They are either computation-intensive or restrict the experimental design to use equal numbers of measurements of all quantities. An alternative approach, whose major disadvantage is that it can be proved to yield the best possible estimates only if the random errors obey a Gaussian distribution, proceeds in two steps. First one calculates a best estimate (typically the mean) and an estimate of the uncertainty (typically the standard error of the mean) for each observed quantity. Then from the set of best estimates the best result is calculated, while the set of uncertainty estimates give (by methods discussed below) an estimate for the overall uncertainty in that result. The two-step approach involves less computation, and, as we will show below, automatically generates explicit estimates of the contributions to the overall uncertainty that result from the uncertainty in each measured quantity. Furthermore, the variation of actual random error distributions from the Gaussian is rarely significant at the level of precision of the error estimates typical of student experiments, as discussed in conjunction with Eq. 9.
Another basis for choosing between the two-step and single-step approaches is essentially philosophical. A "scientific realist" (see Putnam, 1975) holds that the true volume of a rod, to use that example again, is ![]() d2L/4, where L is the true length, and d is the true diameter. In this view, the only defensible, self-consistent belief is that the best estimate of the true volume must be calculated from best estimates of the true length and true diameter. This leads immediately to support for the two-step approach to uncertainty estimation.
d2L/4, where L is the true length, and d is the true diameter. In this view, the only defensible, self-consistent belief is that the best estimate of the true volume must be calculated from best estimates of the true length and true diameter. This leads immediately to support for the two-step approach to uncertainty estimation.
Silverman and Strange, 2004, examine the consequences of the fact that for many functions, f, the shape of the distribution curve for the calculated results will differ from the shapes of the distribution curves for the individual measured quantities. These differences in shape may involve both asymmetry and significant differences in the fraction of the area under the curve at large deviations. Thus, for professional scientific research, where sufficient replications of the experiment may be performed to establish the uncertainties of the individual measurements to better than 1%, a more subtle analysis is called for than we present here.
We consider first the conventional, analytical version of the two-step approach to the calculation of the uncertainty of a derived quantity. We use the best estimates and uncertainties of the various measured quantities used to calculate the derived quantity and assume that there is no correlation of the random errors in the measured quantities. (Taylor, 1985, discusses situations in which correlation of error must be expected.) Let our derived quantity be f, the measured quantities xa, the best estimates <xa> and <f>, and the uncertainties sa and sf. Then the standard result (see, for example, Wilson, 1952, Titus, 1987, or Bevington, 1969) for the uncertainty of the derived quantity reduces to the following, which, like Eq. (8c), is based upon a linear approximation (truncated Taylor series) for the function f:
![]()
For the case of our example of the volume of a rod, we proceed as follows:
![]() V/
V/![]() d =
d = ![]() dL/2 ,
dL/2 ,
![]() V/
V/![]() L =
L = ![]() d2/4 ;
d2/4 ;
![]()
This is intuitively reasonable, since the first contribution is the volume of a "slice" sL thick off the end of the rod, and the second contribution is the volume of an annular layer with a radial thickness sr = sd/2 "peeled" off of the curved surface of the rod.
For some people, the evaluation of the partial derivatives may represent only a small obstacle. Often, however, that exercise dominates the labor of data analysis without producing compensating insight. Furthermore, many intermediate level students have not even taken single-variable calculus, and so can take essentially no benefit from Eq. (14) at all. The desire for another approach is based, then, on the educational benefit of a tractable analysis that is more sophisticated than just keeping track of significant figures.
The finite difference version of the two-step approach is a generalization of Eq. (8), using the concept of "deviated data" described above, just as the analytical version's Eq. (14) was a generalization of Eq. (8c). After calculating the best estimate of the true value (typically the mean), and its uncertainty (typically the standard error of the mean), for each observed quantity, with notation as used previously, we establish three values of the interesting quantity, f:
(15a) f0 = f(<x> , <y>) ,
(15b) f1 = f(<x> + sx , <y>) ,
(15c) f2 = f(<x> , <y> + sy) ,
and then we define
(16) dx = f1 - f0 and dy = f2 - f0 .
We use here the notation "dx" for the "partial deviation in f(x,y) attributable to uncertainty in x." As discussed in conjunction with Eqs. (8) and (9), it doesn't really matter very much whether Eqs. (15b) and (15c) use -sx instead of +sx, etc.. Even if sx is not small, the magnitude of the partial deviation will usually be the same, within the accuracy to which the value of sx is known, using either sign for sx.
We could now derive our estimate for sf, by direct appeal to Eq. (14), even without the example of Eq. (13). To further motivate the analysis, however, it is appropriate to first consider the following. Can we place limits on sf that will hold even if the random errors are correlated? Figure 6(a) shows a geometric construction in which a first line segment is drawn of size |dx|, and from its right end a circle is drawn of radius |dy|, (in the illustrated case |dx| > |dy|). Inspection then justifies the following variations on the triangle inequality:
(17) | (|dx| - |dy|) | ![]() sf
sf ![]() |dx| + |dy| .
|dx| + |dy| .
An equality would hold in the geometrically degenerate cases of colinearity, i.e., statistically speaking, if there were complete positive or negative correlation between the errors in x and those in y. The lower limit holds if the errors in x always offset those in y; the upper limit holds if the errors in x always reinforce those in y.
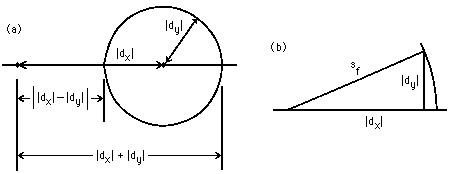
Figure 6. Compounding uncertainties from two sources. (a) The extreme limits, for complete + or - correlation of the random errors. The circle, of radius = |dy|, is offset from the origin by |dx|. (b) The most sensible estimate in the absence of correlation; the arc has radius sf.
For those who are familiar with multivariable calculus, we may use Eqs. (15) and (16) to provide reasonable approximations for each of the terms of Eq. (14). For those who have not seen Eq. (14), one may heuristically appeal to the orthogonality of "independent axes," draw a right triangle such as Fig. 6(b), with legs dx and dy, and use the Pythagorean Theorem to demonstrate the reasonable nature of the following:
![]()
Equation (18) is known as "adding in quadrature" and it provides a reasonable estimate for the uncertainty in the value of f, if the errors in x and y are independent. As Taylor (1982) makes clear, the rigorous proof of Eqs. (14) and (18) rests on the standard deviation as a measure of uncertainty and assuming that the errors are random and obey a Gaussian distribution. Within the limits of accuracy described by Eq. (9), these are indeed reasonable approximations for most physical measurements.
By considering the right triangle with legs dx and dy, and hence, by Eq. (18), with hypotenuse sf, as shown in Fig. 6(b), the student can see that if one of the partial deviations is even three times larger than the other, then the overall error, sf, will be only very slightly larger than the larger of the two partial deviations. (Good, 1976, goes so far as to propose approximating the value of sf by the single largest term in the sum of Eq. (14).) The generalization of Eqs. (15), (16), and (18) to more than two measured quantities is left as an exercise for the student; see, for example, the analysis of the absorption of X-rays by aluminum in Lab 5 of the author's Experiments on Modern Physics and Ionizing Radiation, as described by Piccard and Carter, 1989.
Accurate estimates of sf, the uncertainty in the derived function f, are possible even if some quantities have been measured only two or three times. This follows from application of the ideas discussed in conjunction with Eq. (9). In these cases, however, it is necessary that the terms for such sparsely measured quantities in the sum of Eq. (14), or their partial deviations of Eq. (16), be small compared to the uncertainty in the other terms or partial deviations. This follows from the fact that sparsely measured quantities may have uncertainties that are known only to within 40%.
Having those sparse terms comparable to the other terms' uncertainties would usually be achieved naturally, since the quantities contributing most severely to sf are precisely those which will reward the experimenter for effort expended in repeated measurements. The thoughtful experimenter will measure sparsely those particular quantities that contribute only modestly to sf.
We have considered whether to calculate values of a derived quantity using the individual results of direct measurements, and seen that such an approach will blur the separation of observation and inference. An estimate of the uncertainty in the derived result based on consideration of the variability of such values will likely lead to a result quite similar to what would be obtained from the methods espoused here. However, the calculation of such an estimate would require more computation than one based on Eq. (18), and would not provide any direct guidance to the experimenter as to the relative importance of the various sources of error.
The two-step approach, whether by Eq. (14) or by Eq. (18), preserves the distinction between observation and inference, which is so vital to the scientific method. Of more practical importance, it also provides a quantitative basis for comparing the various contributions to the overall uncertainty. Since the worst one or two will dominate the uncertainty in the derived quantity, the experimenter who performs the two-step calculation will be directed to the easiest way to improve the precision of the experiment. This permits teachers to balance the typically set-piece nature of instructional experiments by directing the student to consider and to discuss both the relative importance of the several sources of error, and the steps that might sensibly be taken to reduce the impact of the most important ones, if the experiment were to be replicated or re-designed. This communicates a more realistic flavor of experimental science, with its preliminary trials, refinements of technique, and so on.
One can always reduce the impact of experimental uncertainty by taking more measurements, increasing N. If only a few measurements have been taken, this can easily provide significant reductions in the uncertainty for modest investments of time and effort. However, because the standard error of the mean declines according to 1/![]() , any measurement would have to be repeated 100 times in order to provide one more significant figure in the result than could be obtained from a single measurement, and would have to be repeated 10,000 times in order to provide two more significant figures than could be obtained from a single measurement: there are diminishing returns to further investments in time and effort simply repeating the measurement.
, any measurement would have to be repeated 100 times in order to provide one more significant figure in the result than could be obtained from a single measurement, and would have to be repeated 10,000 times in order to provide two more significant figures than could be obtained from a single measurement: there are diminishing returns to further investments in time and effort simply repeating the measurement.
In most situations, the experimenter will quickly achieve a state where the best return on the investment of further time and talent to improve the results will be by re-design of the experimental procedure or equipment, so that it is intrinsically more accurate. We saw an example of this with the Franck-Hertz experiment: including the series resistor in the filament circuit permits operation at the lowest possible cathode temperature, imparting the minimum random thermal fluctuation to the electron's initial energy.
Equation (14), based as it is on the first partial derivatives of a truncated Taylor's Series approximation to f, and Eq. (18), based on the first-order differences of Eq. (16), are both reasonable approximations to use for estimating the uncertainty of a derived result. They are identical in the limit of small errors, and surely comparably accurate even if the errors are large. Their adequacy is especially clear in light of the difficulty of establishing exact values for the uncertainty of each directly measured quantity.
The choice between the analytical and the numerical approaches should be made on the basis of convenience. For some people, and in some situations, it will simply be less bother to figure out the partial derivatives and use Eq. (14); often, however, it will be less bother to recalculate with deviated data a few times, subtract, and use Eq. (18). If you reduce the burden of calculation, you will have more time to spend learning physics.
Graphs are very powerful tools for describing succinctly the results of observations and physical experiments. We may perform an experiment with certain mechanical objects and measurement standards, such as stop watches and meter sticks. Words serve to describe an experiment, which might have as its objective the understanding of how a particular event or effect is influenced by various factors. We vary one parameter at a time and gather numerical data which indicates how this parameter affects the measurement of interest. Plotting our results gives us a graph, and we generally try to find a way to make this plot such that the data points fall along a simple curve (such as a straight line). The algebraic equation for this curve then gives us a simple relationship governing the experiment in question. It summarizes both the data and the graphical information in simple form. If there are several independent variables, varying them individually will eventually lead to an algebraic equation relating all of them, if the relationship is indeed that simple. Recent research has provided important insights into the details of human visual perception of graphically presented data (see Cleveland and McGill, 1985 and Tufte, 1983).
A very common feature of laboratory work is fitting straight lines to experimental data or to simple functions of experimental data. (For example, a plot of mass vs volume dispensed from a burette, or a plot of volume vs (1/pressure) at constant temperature.) The straight line approach has the major advantage of easy precision compared to drawing curved lines: it is very difficult to determine the equation for a curve by inspection, but a straight line leads directly to a simple algebraic equation. It is for this reason that it is so common to plot one simple function of experimental data versus another, in order to achieve a straight line plot.
Having found the best straight line for a set of data, one may then determine the slope and one or both of the axis intercepts of that line. Often the values obtained can be interpreted using a theoretical explanation for the experiment. Sometimes a calculated "best fit" line will be determined, as discussed in Section F, but simple graphical techniques are very useful in many applications.
For example, the theoretical formula for the position of a cart accelerating from rest down an inclined plane is
where g is the acceleration caused by gravity and ![]() is the inclination of the plane from the horizontal. A plot of a particular set of experimental values for d versus t is a rising curve, as illustrated in Fig. 7a, but it is not clear from inspection whether the curve is actually a parabola nor whether it agrees with the formula above. To make comparison simpler, we calculate for each data point the value of t2 and plot as shown in Fig. 7b. Note how the horizontal axis is labeled in this case. With a ruler, a straight line is drawn on the graph as close as possible to all the points. (Whether to force the line to go through the origin will depend on whether it is intrinsically an exact point.) The degree to which the data are consistent with the equation represented by that line is shown by how close the points are to the line.
is the inclination of the plane from the horizontal. A plot of a particular set of experimental values for d versus t is a rising curve, as illustrated in Fig. 7a, but it is not clear from inspection whether the curve is actually a parabola nor whether it agrees with the formula above. To make comparison simpler, we calculate for each data point the value of t2 and plot as shown in Fig. 7b. Note how the horizontal axis is labeled in this case. With a ruler, a straight line is drawn on the graph as close as possible to all the points. (Whether to force the line to go through the origin will depend on whether it is intrinsically an exact point.) The degree to which the data are consistent with the equation represented by that line is shown by how close the points are to the line.
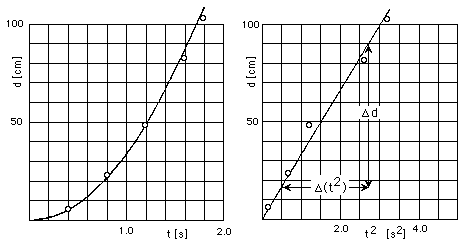
Figure 7: Graphing Experimental Data. For an accelerating cart,
(a) Distance versus time; (b) Distance versus time-squared.
The general equation for a straight line is
where y(0) is the value of y when x = 0 (the y-intercept) and m is the slope. The slope is the ratio, ![]() y/
y/![]() x, of the vertical rise,
x, of the vertical rise, ![]() y, to the corresponding horizontal run,
y, to the corresponding horizontal run, ![]() x, between any two points of the straight line. From Fig. 7b, the slope in our example is found to be
x, between any two points of the straight line. From Fig. 7b, the slope in our example is found to be
On the other hand, we predict the slope to be
If these data were taken with ![]() at 4 degrees, then the experimental value of g found from these measurements is
at 4 degrees, then the experimental value of g found from these measurements is
g = (2*34 cm/s2)/(0.070)
g = 970 cm/s2 ,
The range of data values for each axis will determine whether to include the origin or not, and what scale to use. The major principle is to have data points plot out near to two diagonally opposed corners: spread the graph to cover most of the page. This reduces the impact of drawing error, pencil line width, etc. Quick visual interpretation of the graph is much easier if the origin is on the page, but this may be overshadowed by the need to use scales fine enough to display variations in the data. The scales should be chosen for easy interpolation when plotting the data (scale by two's, for example, or five's, NOT by seven's or nine's). The same scale need not be used on the two axes. The independent variable (the cause, or the one directly controlled) should be plotted along the horizontal axis and the dependent variable (the observed effect) along the vertical axis. The axes should be labeled by names or variables related to the situation being analyzed (not just as "x" and "y"), with the units of measurement, and with the appropriate scale divisions. The numbers should increase from left to right and from bottom to top. The graph should be labeled with a title that indicates the conditions of the experiment. Each data point should be surrounded by a circle, or if several related sets of data are being graphed together one set may have circles, another set triangles, etc..
If the precision of the data is known, error bars may be drawn, parallel to one or to both axes, showing the confidence limits. (This is often reserved for formal presentations.) If all points are essentially equally precise, error bars need be drawn only for a few, noting that these are typical. If error bars are drawn, identify the nature of the confidence interval (s, PE, 95% etc.).
A straight line or a hand-drawn smooth curve should be drawn through the plotted points. The curve need not pass through all the points, but should be drawn in such a way as to fit the points as closely as possible; in general, as many points will be on one side of the curve as on the other.
The idea is simple, but care does need to be taken. You should draw the line that best represents the data as a whole. Do not give undue weight to any particular points, especially the end points. The line is not apt to pass exactly through the first or last data points, except in special cases, but for straight lines will pass through the point whose coordinates are the respective mean values, if the data are good. Your line should be placed so that its height is right (roughly equal numbers of data points at any given distance above the line and below it), and so that its slope is right (no trend for the data points to be above the line at one end and below at the other end). One or two points may fall quite far from the line that seems best for the bulk of the data; do not shift your drawn line to try to come closer to such aberrant points (but see the discussion on discarding data, near the end of Section C).
Again we have a simple idea that needs careful execution. Your drawn line should extend beyond the data points, from very near one corner of the paper to near the diagonally opposite corner. (This extrapolation does not imply that the line is valid beyond the data, it just reduces your error in finding the slope of the particular line you have drawn.) Pick two points on that drawn line, one near each end, and estimate their coordinates from the graph. Probably the most effective way to show what you have done is to draw arrows on the graph pointing to the points you have chosen from an ordered pair giving their coordinates (with units!). Do not write on the drawn line nor within a grid spacing of it, lest you obscure the very part of the graph you need to use for precise estimations. Do not clutter the graph with the rest of the calculation. Using the coordinates and recalling the point-slope form for a linear equation, you can determine slope and intercepts. In order to get the most accurate results, do not choose points that are data points, nor points at which two grid lines intersect the drawn line. It will simplify your work, without introducing bias, if you follow the example of Fig. 7(b), and choose points where the drawn line intersects one grid line between two of the perpendicular grid lines. Forcing yourself to estimate at least one coordinate enhances your intuition for the number of significant figures in your results.
To get a good handle on the precision with which your data have determined the slope and intercepts, you need to consider not just the best fit line, but also "worst believable" lines. If your data all fall very close to the best line, you should either use the numerical methods of Section F to estimate uncertainties, or make a Xerox copy of the graph with the data plotted, before drawing the best fit line. You use this copy for estimating limits on the slope or intercept. The lines you draw on the copies are the worst believable lines: lines that define the extreme values of slope and intercept that are compatible with the data. That is, you draw one line which is too steep to be representative of the data, but as shallow as it can be while still being clearly too steep. Similarly, draw a line which is too shallow. (These two lines can reasonably be drawn on the same paper, since they will ordinarily be well separated. If there is enough scatter in the data, they can be drawn on the original graph without interfering with each other or with the best fit line.) The steep and shallow lines should cross each other somewhere near to the middle of the data.
If an intercept is of interest, one must draw lines that will give intercepts which are too high, and too low. You want to be able to say, "The odds are about twenty to one that if other people do the experiment with the same equipment, and draw their best fit lines decently, that they will find a slope (or intercept) between these two values." In the usual case of four to a dozen points, the worst believable lines should deviate from the best line, at the ends of the range, by about as much as the typical scatter of the data points from the best line.
It is difficult to relate the error limits established by this graphical analysis to the error limits established in other cases by using numerical methods (standard deviations, etc.). Usually your judgment as to how far off the line must be to be "clearly not really representative of the data as a whole" will establish limits that are about two standard deviations on either side of the best estimate (that is, standard deviations for the distribution of best fit lines from many replications of the experiment). Thus if you are in the habit of quoting quantities plus or minus one standard error of the mean, it is sensible to quote the slope or intercept with a plus or minus figure that is one quarter of the difference between your two limiting values. (This is compatible with the figure of twenty to one odds that was mentioned in the previous paragraph; see Table I.) Most people learn the graphical techniques well enough to get within a factor of two of the objective numerically-determined standard error. Bearing in mind the uncertainty of any error estimate, this is quite adequate for most purposes. Lichten (1989) has discussed alternative graphical methods for estimating the uncertainties.
In those cases where the data are not linearly related, it will often be useful to establish the trend of the data, as well as the location of any minima or maxima. The following discussion is in three parts: first deciding where to draw the curve, second, the techniques by which we can hand draw the curve where we want it to be, and third, establishing extreme values.
Deciding where we want to draw the line is easy in cases where the data is "rich," cases in which each "swing" of the curve has many data points. Then we can readily convince ourselves which variations are real and which are errors of measurement. We draw the line to the central tendency of the data, not following each variation in individual measurements. Our job is more difficult in cases of "sparse" data, cases in which the curves of the trend are suggested by the data but few swings of the curve have more than one or two points. In these cases the best approach is to draw a curve that is less extreme than the data on each swing.
Of course, if there is a theoretical basis for expecting a particular shape curve, one should examine the data to see if they seem to conform to or conflict with the expected shape. A test of whether a given curve is a reasonable representation of the data is to count the numbers of consecutive data points that fall on the same side of the drawn line. Any long "run" of points on the same side is cause for suspicion; having two or three long runs is a basis for very strong doubt.
The key trick for hand-drawing smooth curves is to turn the paper so as to place your hand, wrist, and elbow on the inside of the curve. For those parts where the radius is large, the whole arm pivots about the elbow; for medium radius portions, the hand pivots about the wrist; for tight curves, and to "fudge" on the others, flex the fingers.
The graphical technique to establish extreme values from data that were taken without being specifically adjusted to land on the extremes requires that the line be drawn paying attention to the data points on either side of the extreme value recorded. As we know from the calculus, the curve will have a horizontal tangent at each extremum. If the points on either side of the extreme observed value are equal, then the peak should be drawn at that value. If two points are equally high, the peak should be drawn halfway between them. If, on the other hand, there is a highest point, but the two "shoulder" points are not equally high, then the peak should be located between the highest observed point and the higher of the two shoulder points, and will therefore be higher than the extreme observed point.
At times the measured quantity is not the interesting, fluctuating quantity whose extrema you seek but is a combination of the interesting quantity and a more slowly varying "background" trend. The calculus again comes to our rescue, informing us that the extremum of interest occurs where the tangent line to the smooth curve for the measured data has the same slope as the background trend.
There are two situations that call for a numerical approach to line-fitting: when the fit is very good it is inconvenient to make the graph on a large enough scale to reveal the scatter, and when the fit is poor it is easy to introduce bias in the selection of the "best fit" line and in the error evaluations. In other words, the two major advantages of numerical methods are first, freedom from bias, and second, well-defined estimates of the degree of uncertainty in the slope and intercept values generated. The major disadvantage of the numerical approach is that it often will not catch even a gross blunder in the data. For this reason it is especially bold to use numerical methods without first graphing all of the data and inspecting it for blatant mistakes. Graphs are also easier to interpret "at a glance" than lists of parameter values, and so are often displayed in reports, even though numerical methods provide the basis for the quantitative conclusions.
It is now common to find hand calculators preprogrammed for the calculation of the best fit line's slope and y-intercept. Few, if any, are preprogrammed to estimate the uncertainty in those parameters. A programmable calculator or a computer can be used quite easily to calculate the parameters and their uncertainties; see Appendix E. The equations and their philosophical justifications are developed in many statistics texts; one very useful book is Bevington (1969, chapter six for line fitting). As discussed by Bevington, the underlying method is "maximum likelihood," and the procedure that results is known as "least-squares line fitting": the sum of the squares of the y deviations of the measured points from the fitted line is smaller than would be obtained with any other line. To put this in mathematical terms, we write the predicted dependent values, y'i, as a function of the measured independent values, xi, and the fitting parameters, a and b:
Under the specific conditions described, for example, by Bevington, the "best fit" values of a and b are then those that minimize the sum
Depending on the situation, other criteria of "best fit" might be more sensible, for example, minimizing the total of the squares of the shortest distances from the data points to the chosen line, or doing either minimization with different weights for different points or for the two variables (see Macdonald, 1975; Reed, 1989; Heald, 1992; Reed, 1992; Macdonald, 1992; and the references they cite).
The numerical line-fitting techniques discussed here and in Appendix E can also be generalized to deal with situations in which the functional relationship between the measured quantities is non-linear. Fitting is accomplished by adjusting the values of one or more parameters in the functional relationship. The criterion chosen for "best-fit" is minimization of a non-negative "loss function," such as the ![]() illustrated above. (It may not exhibit all of the classical properties of the statisticians' "chi-squared" distribution, but in some cases it does, which motivates our choice of notation.) In the simple linear case illustrated above, one may use the calculus to deduce analytical expressions for the optimum values of the parameters. In the general case this is not possible. Many strategies are possible for exploration of the possible parameter values, including both pseudo-random ("Monte Carlo") and systematic approaches. All the common approaches are trial and error: the loss function is evaluated repeatedly from the experimental data using particular combinations of parameter values, and the results compared to prior evaluations. See Bevington, chapter 11, for a discussion of a number of alternative methods.
illustrated above. (It may not exhibit all of the classical properties of the statisticians' "chi-squared" distribution, but in some cases it does, which motivates our choice of notation.) In the simple linear case illustrated above, one may use the calculus to deduce analytical expressions for the optimum values of the parameters. In the general case this is not possible. Many strategies are possible for exploration of the possible parameter values, including both pseudo-random ("Monte Carlo") and systematic approaches. All the common approaches are trial and error: the loss function is evaluated repeatedly from the experimental data using particular combinations of parameter values, and the results compared to prior evaluations. See Bevington, chapter 11, for a discussion of a number of alternative methods.
The simplest algorithm is to select a set of values of each parameter (usually equally-spaced, forming a uniform grid in parameter space) and evaluate the loss function for every combination of parameter values. The lowest observed loss function is presumed to be close to the lowest possible, and the particular combination of parameter values that produced it is taken as the best fit. A generalization is to repeat the method, taking a grid of paramter value combinations that spans a smaller region, but more finely divided. Iterating will clearly take you as near as you like to the parameter values that minimize the loss function for the particular data set. However, the fluctuations to be expected if the experiment were replicated clearly imply that excessive precision in the fitting is a waste of effort.
A more sophisticated approach is to start exploring the grid implied in the previous approach, but to keep track of the successive values of the loss function as you move along a row or column of the grid, changing one of the parameter values sequentially. As soon as the loss function increases, you step back, freeze that parameter value for this cycle, and begin to modify another parameter's value. Instead of evaluating the loss function at each grid point within the spanned volume, you will have done so along a path that encompasses far fewer points, and hence much less calculation. There is, however, the possibility of falling into a "local minimum" rather than the "global minimum" in the loss function that you seek. However, loss functions do not typically exhibit severe local minima, so this is not usually a problem.
Bevington also presents two algorithms based on evaluating the loss function at a number of closely-spaced grid points, so as to be able to estimate the derivatives of the loss function with respect to each of the parameters. In this way, it is possible to strike out along a diagonal in parameter space, rather than moving parallel to the axes as described in the previous paragraph. This direct motion can be expected to reduce significantly the number of times that the loss function must be evaluated. The simpler of these two algorithms estimates the first derivatives, and hence is approximating the surface of the loss function by a plane (a first-order Taylor expansion of the loss function as a function of the parameter values). The more complicated algorithm estimates both the first and the second derivatives to use a second-order Taylor expansion of the loss function, and hence is approximating the surface of the loss function by a paraboloid of revolution. This does require more initial calculation, but in practice the savings achieved by heading more nearly directly toward the actual best fit suffice to make up for the initial effort. (Except if the starting point of the calculation is very far from the best fit; for that reason, some programs are written to use the first-order method for one cycle, and the second-order method from then on.)
Monte Carlo methods can take either of two approaches: a pre-calculated grid, using parameter values that are chosen using pseudo-random numbers instead of uniform spacing, or successive points with the displacement from the previous trial chosen pseudo-randomly. The latter case might be described as a pseudo-random walk through parameter space. At each trial, if the new value of the loss function is higher, the next trial is taken from the original position, whereas if the new value of the loss function is lower, the next trial is taken from the new position. If the decision about whether to take the next trial from the new or old position is itself randomized, rather than being rigidly determined simply by comparing the loss function values, the method is described as using "simulated annealing." These more exotic strategies involving simulated annealing are particularly robust for selecting the global minimum in the loss function even when there are many local minima. See Press, et al, 1988, section 10.9, and the references cited there.
Care must be taken when considering the application of such numerical approaches to be sure that the assumptions of the analytical derivation supporting the loss function chosen, and the minimization algorithm, are in fact valid for the data at hand. For example, the usual linear least-squares fitting formula is only valid in the case that the independent variable's values are known exactly, and that the absolute (not relative) uncertainties of the dependent variable's values are the same for all data points. A relatively simple extension, included in Appendix E, covers the case where the dependent variable's uncertainties differ from point to point, but are all known.
When regression techniques are generalized to situations that involve more complex relationships, this usually involves the user writing a program specifically for the application. In linear cases, numerical methods are more typically used by running commercial statistical software. Such packages as MINITAB and SPSS provide for "linear regression analysis," in many cases including a variety of sophisticated tests seeking to identify and call to the user's attention any aberrant data points.
One test for adequacy of the theory that claims a particular functional relationship among the measured quantities is to examine the number of "runs." In the two-variable case, a "run" is a sequence of observations with the same sign of the difference between the observed and the predicted values. (With more than one independent variable, the space of data points can be divided into compact regions where the error of prediction has the same sign.) The maximum number of runs is the number of data points (alternating signs of errors). If the discrepancies are truly random, and hence the theory used for the predictions is adequate, then the number of runs would be somewhat less than the maximum. Too large or too small a run count is an indication of significant shortcomings in the theory. This comment applies whether the situation involves a linear fit or a more complex functional relationship between the measured quantities.
Radioactive decay and resistor-capacitor filter transient response are typical of situations in physics calling for the analysis of data that follow an "exponentially decaying" curve. In biology, the removal of medications or toxins from the blood by the liver follows the same mathematical pattern. The analysis of such experimental data may be done with graphical or numerical methods. We deal with the following equation:
![]()
where X(0) is the value at t=0 of the decay rate, remaining number of atoms, voltage, current, etc., and ![]() is the "mean lifetime" or "time constant" of the decay. In situations where the natural physical quantity "decays" to a non-zero value (e.g., cooling a finite-sized sample by contact with a constant-temperature reservior), Eq. 19 can be applied with X(t) being the difference between the value at time t and the final value. We consider two particular consequences of Eq. 19. First, the graphical analysis of such data, and second, the relationship between mean- and half-lives. Taking natural logarithms of both sides of Eq. 19 gives
is the "mean lifetime" or "time constant" of the decay. In situations where the natural physical quantity "decays" to a non-zero value (e.g., cooling a finite-sized sample by contact with a constant-temperature reservior), Eq. 19 can be applied with X(t) being the difference between the value at time t and the final value. We consider two particular consequences of Eq. 19. First, the graphical analysis of such data, and second, the relationship between mean- and half-lives. Taking natural logarithms of both sides of Eq. 19 gives
(20) ln(X(t)) = ln(X(0)) - (t/![]() ) .
) .
This can be rewritten more suggestively as follows:
(21) ln(X(t)) = ln(X(0)) + (-1/![]() )t .
)t .
Thus we can see that a graph of ln(X(t)) vs t should display a linear form with slope equal to -1/![]() , and t = 0 intercept of ln(X(0)). The logarithm has no units, so the slope must have units of 1/sec, while
, and t = 0 intercept of ln(X(0)). The logarithm has no units, so the slope must have units of 1/sec, while ![]() has units of sec. Numerical line-fitting techniques may also be used. For radioactive decay data, the uncertainty can usually be evaluated from the data (
has units of sec. Numerical line-fitting techniques may also be used. For radioactive decay data, the uncertainty can usually be evaluated from the data (![]() , based on the Poisson distribution) so that the usual assumption of equal errors should not be used for the numerical method.
, based on the Poisson distribution) so that the usual assumption of equal errors should not be used for the numerical method.
The calculation of the half-life, T, in terms of the mean life, ![]() , proceeds from T's definition as "the duration of the time interval required to reduce X to half the value it had at the start of that interval"; using Eq. 19:
, proceeds from T's definition as "the duration of the time interval required to reduce X to half the value it had at the start of that interval"; using Eq. 19:
![]()
Taking the natural logarithm of the middle and right expressions of Eq. 22 gives
(23) ln[X(0)] - ln(2) = ln[X(0)] - (T/![]() ) ,
) ,
which immediately simplifies to
(24) - ln(2) = -(T/![]() ) .
) .
Hence, finally,
(25) T = ![]() ln(2) = (0.69315)
ln(2) = (0.69315)![]() .
.
A little algebra from Eq. 25, substituting into Eq. 19 and then simplifying, will give Eq. 26, which could have been taken as the definition of the half-life, and which you may find easier to remember than Eq. 25:
![]()
When it is more convenient to use semi-log graph paper (which uses base 10 logarithms), the slope, m, is computed in "decades" per second, and hence
(27) 1/m = ![]() ln(10) = (2.3026)
ln(10) = (2.3026)![]() .
.
When an analog quantity is digitized in the measurement process, there are several contributions to the uncertainty of the measurement:
With common commercial ADC units, each of the third, fourth, and fifth contributions are likely to be on the close order of ± half of a least-significant-bit in the digitized output.
The transducer and the ADC may also exhibit mis-calibration (whether consistent or influenced by instrument temperature or other variable conditions), contributing to systemmatic errors that may well be an order of magnitude larger than a least-significant-bit.
In many experimental situations, the ADC is a separate unit, so it is useful to consider the first two contributions together and the third and fourth contributions together. The variation in the actual analog quantity and the noise from the transducer together result in a variable signal reaching the ADC unit. The ADC's input-stage analog noise and the non-linearity in the analog-to-digital conversion process result in a less accurate value, but the ADC also limits accuracy because it will have a fixed number of possible output values.
The analog signal is a continuous variable, but an ADC output is always a discrete number (whether transferred electronically as a binary number, or displayed as a decimal value on a multi-segment display). This rounding-off can be thought of as a process of compounding the other sources of error with an error whose distribution function is flat-topped with a width corresponding to the smallest step displayed (or recorded) in the output.
If multiple measurements are made to determine the average value of a signal that varies over a range large compared to the least significant bit reported, the round-off error should be expected to "average out" better and better as more measurements are included in the average. If, however, the signal varies over a range small compared to one least significant bit, the result will always be the same (unless that small range spans the boundary between two values), and the average will be wrong by the round-off error, no matter how many measurements are taken.
For this reason, it is common design practice for ADC input stages to contribute noise comparable to one-half of the least significant bit digitized: a single measurement will be slightly degraded, but a long series of measurements will average much closer to the correct value. (This is sometimes referred to as "dithering"; the ADC will also be cheaper since design and construction for low noise is not trivial.) However, if the natural variations in the quantity being measured and the noise in the signal from the transducer are together yielding fluctuations on the close order of one-half of the least significant bit digitized, then a modest but real improvement will be achieved by using a more expensive ADC, designed to digitize to more bits, even if only the same number (of the most significant) bits are recorded (Piccard, 1979). The more precise ADC can reasonably be expected to contribute much less noise than the rest of the electronics, and yet the variation and noise that are present from other sources will suffice to ensure the averaging-out of the round-off to however many bits are reported. The more precise ADC will likely also exhibit smaller non-linearity errors.
When the "same" quantity is measured repeatedly, that may be done simply in order to average the results. However, it is often the case that repeated measurements are made in order to examine the way in which that quantity is changing with time or space: digitizing an electronic signal that represents a sound is usually done by measurements that are periodic in time; digitizing a photographic image is usually done by measurements that are periodic in space.
In any situation involving sampled data, care must be taken to measure the value often enough to follow the variations that occur in the input signal. For example, it is obvious that measurements of an electrocardiogram signal taken once every 3 seconds would convey no useful information about the subject's medical condition. On the other hand, measurements made every microsecond would surely show every detail of clinical interest throughout each heartbeat, but would generate so much data as to swamp any sensible data-analysis system.
The rigorous analysis of data sampling is due to Harry Nyquist (1928b). Nyquist had earlier (1927, 1928a) demonstrated that the noise discovered by Johnson was due to the Brownian motion of the gas of valence electrons in the interior of the conductor. Nyquist also provided us (1932) with the analysis of stability vs spontaneous oscillation in amplifiers with positive feedback. We will discuss the Nyquist sampling theorem briefly after first examining a few specific cases.
Consider what sorts of signals can be accurately measured with a fixed sampling rate. As is shown in Fig. 8 (a), if the input is a sine-wave of frequency exactly matching the sampling rate, then the measured value will be the same each time. (The actual value depends, of course, on the amplitude of the signal and on the phase at which the measurements are made.) The appearance is thus of a DC value, as suggested by the dashed line in Fig. 8 (a).
Figure 8: (a) Signal frequency equal to sampling frequency.
(b) Signal frequency of 0.8 * sampling frequency.
As is shown in Fig. 8 (b), if the signal is a sine-wave of frequency slightly above or slightly below the sampling rate, the measured results will vary slowly as their phase shifts gradually with respect to the input waveform. As shown by the dashed line in Fig. 8 (b), the numbers then would be seeming to indicate a very low frequency signal when none was in fact present.
Continuing with the analysis for a fixed sampling rate, consider the result with an input of frequency half the sampling rate. As shown in Fig. 9 (a), the measured value will alternate between two values of the same magnitude but opposite sign, the magnitude depending on the signal amplitude and the phases at which the measurements are being taken. The signal appears to be of the frequency that it actually is, but it may appear to have any magnitude between zero and the full magnitude of the signal. The phase of the actual signal cannot be determined from the data.
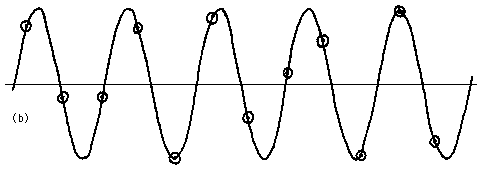
Figure 9: (a) Signal frequency of 0.5 * sampling frequency.
(b) Signal frequency of 0.4 * sampling frequency.
If the input signal is of frequency close to, but not equal to, half the sampling rate, the results will indicate a signal of frequency equal to half the sampling rate but of varying amplitude. Consider cases in which the signal frequency is only very slightly different from half the sampling frequency. In that case the successive samples will be taken at nearly opposite phases of the signal, gradually drifting from the peaks to the zero-crossings, and back. Thus, the amplitude can be expected to vary from zero to full. Figure 9 (b) shows a case in which the signal frequency is about 0.4 of the sampling frequency. It provides graphic proof that casual observation will not suffice in such cases to go from the measured values to the actual waveform present.
We see therefore that when the ADC is presented with signals having frequencies near to or above half the sampling rate, the results will be either unpredictable or surely misleading. This process, by which steady sine-wave signals of one frequency masquerade as very different signals, is known as "aliasing." In order to make meaningful measurements by digitizing a waveform we need not only to have enough significant figures (bits), but also must avoid combinations of sampling rate and waveform shape (frequency content) that would provoke aliasing.
Aliasing is typically prevented by a combination of three techniques:
The two common approaches to designing and constructing input filters are:
The trade-off here is between excessive amounts of data in the first case, and a complicated (and therefore expensive and unreliable) filter in the second case. It is possible to make an elaborate low-pass filter that provides a pass-band response that is flat within less than 1 dB out to the cut-off frequency and yet attenuates by at least 60 dB any signal more than an octave beyond the "cut-off frequency." This is expensive and sounds quite precise, but there are a number of issues:
Whatever filter is used, the low-pass characteristic is invariably coupled with a gradual settling in toward the final value of the output following any sudden change in the input potential. This means that accurate, precise measurement of the potential immediately after any large change or spike in the input will be difficult for some period of time. Many experiments involve measuring responses to stimuli that will also produce a brief major artifact in the signal circuits; an unfortunate choice of ADC input filter may then hamper or prevent useful measurements of interesting prompt responses to that stimulus.
The Nyquist sampling theorem states that IF the signal being sampled is bandwidth-limited, that is, if there is a frequency at and above which all of the Fourier coefficients are identically zero, then the signal can be accurately represented by evenly spaced samples at the rate of at least two per cycle of that high frequency limit. The practical problem is twofold. First, many signals have a minor high frequency component that must be filtered out if the data rate is to be kept within bounds. Second, virtually all signals will contain some broad-spectrum noise, which must also be filtered out if it is not to be compounded, by aliasing, with the noise actually present at the lower frequencies where the signal has significant components.
The requirement of bandwidth-limiting should be considered both in cases involving truly or nearly periodic signals (wave packets of extended duration, perhaps extending over the whole duration of data taking), and also in cases involving one-time-only events (transient signals). The spectrum of a wave packet will typically exhibit a broad peak centered about the nominal frequency. The width of that peak will be inversely related to the duration of the packet. If the individual cycles have a non-sinusoidal shape, then the spectrum of a perfectly periodic wave of that form will consist of a series of spikes at frequencies that are integer multiples of the fundamental. The result of confining the packet to a finite duration will be to broaden each of those spikes into a peak of non-zero width.
Transient events can be viewed as extremely short duration wave packets, having therefore a spectrum with very broad peaks, and consequently a very high maximum interesting frequency. Common sense, however, is actually adequate to demonstrate the need for a high sampling frequency in such cases: if it only happens once and you don't get a measurement, then you are never going to know about it! Further, if you don't get multiple measurements during the transient, then you won't learn much about the detailed sequence of events.
These appendices are identified by letters that seem whimsical in the context of these Notes on Modern Physics and Ionizing Radiation because they were also used with the author's Notes on Instrumentation Electronics, which are not now available on-line.
These two distributions are relatively simple to describe mathematically and occur in practice often enough to be of particular interest to scientists. The Gaussian distribution is the standard "bell-shaped curve" that shows up repeatedly in statistical analysis. The Poisson distribution, on the other hand, although single-peaked, is not symmetrical. Furthermore, it applies only to situations in which all of the possible results of a measurement are non-negative integers. The Poisson distribution is an instance of a "discrete" distribution, and the Gaussian distribution is an instance of a "continuous" distribution. One speaks of the Poisson distribution as describing the results of some "counting" experiments, and of the Gaussian distribution as describing some "measurements."
Equation 1, below, gives the Gaussian distribution in terms of a formula for the "probability density," ![]() (x). The probability, P(a,b), of obtaining a result between a and b is equal to the area under
(x). The probability, P(a,b), of obtaining a result between a and b is equal to the area under ![]() (x) for that interval, as shown below:
(x) for that interval, as shown below:
For the Gaussian case we have:
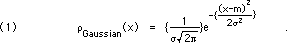
An exercise in calculus demonstrates that m is the expectation value and that ![]() is the standard deviation of the distribution. A little algebra will show you that for the Gaussian distribution the full width is 2
is the standard deviation of the distribution. A little algebra will show you that for the Gaussian distribution the full width is 2![]() at the maximum height times
at the maximum height times ![]() (i.e., at approximately 61% of the maximum height).
(i.e., at approximately 61% of the maximum height).
The Gaussian distribution is important for several reasons. There are in fact many experimental situations for which it seems to be the exact description. Many other situations that are clearly not exactly described by it can still be quite usefully approximated by it. The Gaussian probability density describes many situations in quantum mechanics. Finally, if N measurements are made and averaged, and another N made and averaged, and so on, the distribution for the averages will be Gaussian in the limit of large N, for almost any "underlying" distribution for the measurements. (This last is known as the "Central Limit Theorem" of probability.)
The Poisson distribution is described by Eq. 2, below, which directly gives P(N), the probability of obtaining the result N:
(2) PPoisson(N) = (mN)(e-m)/N! ,
where m (which need not be an integer) can be proved to be the expectation value. Equation 2 cannot be evaluated directly for large values of m or N (on most calculators) because the intermediate numbers are too large or too small. Unlike the Gaussian distribution, the Poisson distribution formula has only one free parameter, m. This means that the distribution's standard deviation, ![]() , must itself be a function of m. Another exercise in calculus demonstrates that
, must itself be a function of m. Another exercise in calculus demonstrates that
(3) ![]() =
= ![]() .
.
Equations 2 and 3 have several significant implications. If the Poisson distribution applies, then it is possible to deduce a firm quantitative estimate of the uncertainty of a result based on a single measurement: if N counts were recorded, one reports N ± ![]() . The relative uncertainty,
. The relative uncertainty, ![]() /m, is 1/
/m, is 1/![]() . This means that in order to improve the relative accuracy, the counting time interval, for example, must be increased so that m, the average number of counts during the interval, will increase. But there are "diminishing returns": in order to halve the relative error, the counting time must be quadrupled.
. This means that in order to improve the relative accuracy, the counting time interval, for example, must be increased so that m, the average number of counts during the interval, will increase. But there are "diminishing returns": in order to halve the relative error, the counting time must be quadrupled.
The probability of observing zero counts is always positive: P(0) = e-m, but recording zero counts is very unlikely if the average number of counts, m, is even as large as five (e-5 = 0.0067, roughly). Finally, as stated above, the Poisson distribution is not symmetrical about the average value, unlike the Gaussian, because N cannot be negative but can be quite large. For very large mean values, m, the Poisson distribution can be closely approximated by a Gaussian distribution with mean m and standard deviation ![]() .
.
A prime example of a situation to which the Poisson distribution applies is radioactive decay of macroscopic samples, which we will discuss here in some detail. In the usual case of medical interest, and in many cases of research interest, there are a large number of nuclei present that could decay at any time, even though only a small fraction of them actually do decay during any given interval. It is precisely such cases of random events in time that the Poisson distribution describes. Another example is the signal from a vidicon-type TV camera tube or a CCD camera or video chip. A typical signal from one picture element is less than one million electrons, a tiny fraction of all the electrons present. Generally, the Poisson distribution applies when the average count is tiny compared to the maximum that could by chance occur.
The intensity of radiation from a radioactive source is typically measured by counting the number of quanta that deliver their energy to a detector during some period of time. If the geometrical arrangement of the source and detector and the efficiency of the detector are taken into account, one can deduce the rate at which quanta are being emitted from the source. From this rate and a knowledge of the half-life of the nuclei one can deduce the number of radioactive nuclei present in the source. To be specific, suppose that with the source present there are Ng counts recorded during a time interval tg ("g" for gross) and with the source absent Nb counts are recorded during tb, ("b" for background). Nb is rarely zero, because of cosmic rays, the presence of trace radioactive isotopes in the detector itself, and noise in the electronics. The gross and background counting rates are denoted Rg and Rb, and we can immediately see that the best estimate of the counting rate due to the source is the net counting rate:
(4) Rnet = Rg - Rb = (Ng/tg) - (Nb/tb) .
A more subtle question is the determination of the uncertainty in the net rate, based on the uncertainties in the values of the two counts and the two measured time intervals.
Is there in fact any uncertainty in the value, for example, of Ng? Truly there should be no question as to the number of counts recorded in a particular measurement, with the possible exception of an event that occurs exactly at an end of the time interval, or of two simultaneous counts. But, the uncertainty in the count value is a concept that involves repeated countings, and these will not all give the same answer, because of the random nature of radioactive decay. One measure of the uncertainty in a count, Ng for example, is the standard deviation of the distribution that describes the counting, ![]() g, or an estimate of it, sg, which clearly will not be zero.
g, or an estimate of it, sg, which clearly will not be zero.
A brief examination of Eqs. II-10 through II-13 indicates that for independent measurements the error in a difference is also the square-root of the sum of the squares of the individual errors. We apply this to the question of accuracy in determining radioactive decay rates:
![]()
where we are using capital S's for the uncertainties in the rates and small s's as uncertainties in the observed counts. In general, each of the S's must be calculated using Eq. II-18; in the common case of a very well-determined time interval, we can simplify the calculation by pretending st = 0, for both tb and tg. We then find the S's easily, as follows:
(6) Sg = sg/tg and Sb = sb/tb ,
where the s's can be found from Eq. 3:
(7) sg = ![]() and sb =
and sb = ![]()
.
Combining Eqs. 5, 6, and 7 we find that the uncertainty in the net counting rate is given by
![]()
which may be "simplified" for calculation as follows:
![]()
If there is uncertainty about the duration of the counting time intervals, then there will be additional terms inside the radical on the right side of Eq. 9, derived from the complete use of Eq. II-18.
We assume data in the form of N ordered pairs, (x,y), with no uncertainties in the x values, and with errors in the y values being one of two types:
(We can deal approximately with any uncertainty in the x value by inflating si into an "equivalent net uncertainty" for each data point. The resulting line will not be exactly the "best fit," but will do quite well for most practical purposes.) In the first case all the points should be equally weighted in determining the best line, but in the second case those points with smaller uncertainties should be counted more heavily.
The easiest procedure is a once-through scan of the data, accumulating the six sums given in Table II. (The notation used there and in Eqs. 2 through 5 was developed for use with a pocket calculator.) From these sums we then compute the slope and y-intercept as well as the uncertainties in the slope and intercept. We fit the data to an equation of the form
(1) y = a + bx .
As discussed by Bevington (1969), the underlying method is "maximum likelihood," and the procedure that results is known as "least-squares line fitting": the sum of the squares of the y deviations of the points from the fitted line is smaller than would be obtained with any other line.
The calculation of the parameters and their uncertainties is based on the values of R0 through R5 as defined in Table II, and uses two intermediate results, D and V, as shown below. The procedure is as follows:
D = R0*R2 - R1*R1 ,
(2) a = (R2*R3 - R1*R5)/D ,
(3) b = (R0*R5 - R1*R3)/D .
Next we define V; for case 1 we have:
V = [ (R4)2 + a2R0 + b R2 + 2(abR1 - aR3 - bR5)] / [R0 - 2] ;
for case 2 we have V = 1. Finally we calculate the parameter uncertainties:
(4a) (sb)2 = V*R0/D ,
sb = uncertainty of slope;
(5a) (sa)2 = V*R2/D ,
sa = uncertainty of y-intercept. An alternative calculation for case 1 can be used in the event that a calculator is available that is pre-programmed to calculate the "correlation coefficient" r:
(4b) (sb)2 = [sy/sx]2 * [(1 - r2)/(R0 - 2)] ;
(5b) (sa)2 = (sb)2* (R2/R0) .
Heald (1992) provides a simple method to improve the accuracy of the calculated uncertainties for cases of small uncertainty (high correlation) where round-off error (for example in the factor [1 - r2]) would otherwise reduce the achievable precision. Essentially, he suggests calculating a first approximation to the slope, subtracting the resulting predicted values from the data, then fitting the residuals, and finally putting it all back together. This would be especially important in cases where the readily-available calculation was limited to single-precision FORTRAN, for example, but might be a significant advantage even in cases where 10-digit calculators are used.
Equations 2 through 5 are reasonable approximations but not the best possible ones in cases that involve major uncertainty in the x values, even if "equivalent net uncertainties" have been used for the s's. (If we use the line to predict y values, the standard error of that prediction will be the square root of V, for case 1.) Round-off errors and data entry mistakes can often be avoided by calculating from data that have had any large power of ten factored out, and any large constant term subtracted; of course the same factor and term must be taken from each point. Equations 2 through 5 are sensitive to round-off error. See the discussion following Eq. II-4.
Standard statistical packages for use with computers frequently implement only case 1. There are some (such as MINITAB) that do provide for case 2, and a few that will routinely use case 2 with the weights automatically selected to pay more attention to the points closest to the line (the so-called "iteratively re-weighted least-squares line fitting"). Such re-weighting is not necessarily justified, especially if you have a basis for believing that all the points are taken by a procedure that gives the same accuracy for each.
Table II: The Sums for Line Fitting | ||
| Sum Symbol | Case 1 | Case 2 |
|---|---|---|
| R0 | N | |
| R1 | ||
| R2 | ||
| R3 | ||
| R4 | ||
| R5 | ||
The above entries use the HTML codes for superscript and subscript for the i's (all subscripts) and the 2's (all superscripts). If your browser does not display them accordingly, you will have to use your imagination! | ||
One interesting feature of human senses is their pattern of regarding equal ratios of stimulation as equal increments of perceived intensity. That is, a 10% increase in sound power levels will sound like an equal "change in loudness," whether the base level is near the threshhold of audibility or of pain. One way of expressing this fact is to say that human senses have a "logarithmic response"; this is a sensible description, because adding equal increments to the logarithms of numbers is equivalent to multiplying the numbers themselves by equal constants. Another instance of logarithmic response of human senses is pitch perception: every time the frequency of a waveform is doubled, the sound is perceived as having risen by one octave.
It is for this reason that the graphical presentation of information so often is done with a "log-log" plot. That is, the physical coordinates on the paper are proportional to the logarithms of the measured quantities, rather than to the quantities themselves. Such plots have advantages in other situations too: if all the data have been measured to some particular percentage uncertainty, then the error bars on the log-log plot will all be the same size, unlike the conventional plot in which the error bars would be smaller for those quantities whose value was smaller. A second advantage is that it is possible to clearly present information spanning a range of many orders of magnitude (depending on the situation this may require a full log-log plot, or only a semi-log plot in which one axis is logarithmic and the other is linear).
(a) Find the gross, background, and net counting rates.
(b) Determine the standard error for each rate.
Dick Piccard revised this file (https://people.ohio.edu/piccard/radnotes/data.html) on October 17, 2012.
Please E-mail comments or suggestions to piccard@ohio.edu.