, and measure the intensity, I(x), of the beam of unscattered, unabsorbed photons remaining at any particular depth, x:
When neutrons collide with nuclei they may bounce off (an elastic collision) or they may stick (an inelastic collision) producing a new nucleus with the same charge (+Ze) but with a mass increased by one "amu" (atomic mass unit) and atomic mass number, A = Z + N also increased by one. If the original isotope was the most massive stable form of that chemical element, then the new isotope will itself be radioactive. If a macroscopic sample is irradiated with neutrons, then eventually some portion of the sample will be transmuted into a radioactive isotope of that element. If the naturally occurring element consists only of isotopes with even numbers of neutrons, then each naturally occurring nucleus may be rendered radioactive upon absorption of a single neutron.
This neutron activation process can be used to produce short half-life isotopes at locations close to where they will be used, so that only a small portion will decay during transportation. Major hospitals often have particle accelerators designed to generate neutrons to be used to create radioactive materials for cancer treatment, or for diagnostic purposes.
Neutron activation can also provide a useful analytical tool for establishing the composition of an unknown sample, since the nature and energy of the resulting radiation will be characteristic of the original elements present.
This technique is applied in one type of airport security luggage inspection bomb detectors, which use thermal neutron activation ("TNA") to detect the anomolously high nitrogen content of high explosive chemicals. Such inspections are far less benign than ordinary carry-on luggage X-ray inspections, since a modest portion of the inspected matter is certain to be rendered radioactive: the radiation persists after the inspection process has been concluded, unlike the X-rays, which are gone at the speed of light as soon as the generator is turned off.
Neutron activation, rather than contamination with fuel or fission products, is the major source of long-term radioactivity in reactor housing vessels for nuclear power plants. In some cases, the radioactivity produced this way from the trace elements in the steel alloy will dominate that produced by activation of the iron atoms, even though they are much more numerous.
Neutron activation can also be used to "dope" silicon crystals to construct electronic devices. The decay product will be in the adjacent column of the periodic table, and if the decay energy is small enough, the daughter nucleus' recoil energy will not break the interatomic bonds that hold it in place within the crystal. Thus the dopant atom will be in exactly the correct location and the crystal lattice will have no defects.
When a beam of photons passes through matter, a variety of interactions are possible, including scattering and absorption as well as undisturbed transmission. The process is random, with each photon independently having some small probability of interacting in any given way with each atom as it passes through the target. In the case of so-called "good geometry," any interaction between the incident quantum and the target removes that quantum from detection as part of the unscattered, unabsorbed radiation, the "main beam." In such cases, one therefore measures and seeks to predict the intensity of the main beam as a function of the thickness of the target. In the case of safety shielding, on the other hand, one must consider scattered and secondary radiation as well as the main beam.
If the detector is a Geiger-Muller tube, or any similar device that does not permit distinguishing these other radiations from the main beam, and if the geometry permits significant numbers of scattered or secondary quanta to reach the detector, then the prediction of the counting rate as a function of absorber thickness is complicated. The simpler theory that is appropriate in the case of good geometry will be developed first.
We consider a monochromatic beam (that is, a beam composed of photons all of which have the same energy, and therefore the same frequency, wavelength, and, if visible, color) passing through successive layers of thickness , and measure the intensity, I(x), of the beam of unscattered, unabsorbed photons remaining at any particular depth, x:
where 
is characteristic of the material and photon energy. The relationship must be of this form; because all the photons are identical, a specific fraction of the incoming photons will be scattered or absorbed in each layer, and clearly the thicker the layer, the more will interact. The increased absorption with increased thickness will be linear (
) only in the limit of thin layers, for which << 1. (In essence the atoms of the front of the layer must not shield the atoms at the back of the layer, and there must be no double-scattering.) See also Eqns. I-16 through I-21 in the discussion of exponential decay of radioactive materials. Algebraic manipulation of Eq. 1 leads to the following:
in other words, the rate of change of the intensity is proportional to the intensity. Hence, by the calculus,
or
for monochromatic photons, with definitions of symbols as below, following Cember (1969 page 122 and following):
I(0) = incident intensity;
x = absorber thickness;
I(x) = intensity after passing through an absorber of thickness x;
T(x) = transmission probability of an absorber of thickness x
The transmission probability is defined such that a transparent object has T = 1, and an opaque object has T = 0.
There are four standard ways to specify the absorber thickness and hence four corresponding ways to specify the absorbption coefficient:
.
1 barn = area of a square 10 Fermi on a side = 100 square femtometer, the approximate physical cross-section size of a nucleus with a 6 fm radius:
The mass density, in grams/cubic centimeter, the atomic weight, in grams/mole, and Avogadro's Number, in atoms/mole, can be used to convert among these four methods of measurement.
Another common way to describe the passage of radiation through matter is in terms of the mean distance traveled through the absorber, the "mean penetration depth," D. In exact analogy to radioactive decay (e.g., Eqs. I-20 and I-21), we can write:
(4) D = 1/ .
Because D is the mean penetration depth, we expect that many photons will be absorbed or scattered before reaching that depth, and that many will penetrate significantly farther than D. Figure 6 shows an example of exponential absorption, from which we can learn more about the significance of the mean penetration depth, D.
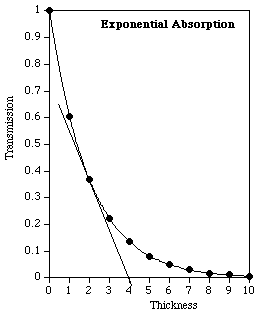
Figure 6: Exponential absorption of photons, with linear scales. The data are for a mean penetration depth of 2, and the thickness extends to five times that value.
An intuitive feel for the significance of D may be more easily grasped in two related ways using Fig. 6:
The curve starts at T = 1, with zero absorber present, and has fallen to a value of 0.37 at x = 2, as advertised.
This means that in fact the majority of photons do not even penetrate as far as D.
The straight line is tangent at x = 2, and extends to intersect the zero-transmission axis at x = 4, further confirming the stated value of D = 2.
A quick look at Fig. 6 might lead you to believe that the transmitted intensity falls to zero after a thickness of five or six times the mean penetration depth. Indeed, the transmission does get quite small, but it does not fall to zero, ever, although the transmitted intensity will eventually fall below the natural background level for that location. This is most easily seen by inspecting a so-called "semi-log" plot, such as Fig. 7, in which the transmission is displayed on a logarithmic scale, where equal increments vertically on the paper represent equal ratios (here, each grid line represents a reduction to one-tenth the value at the grid line above it).
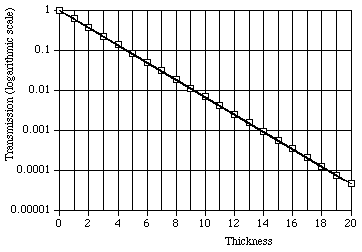
Figure 7: Exponential absorption of photons with logarithmic scale for transmission and linear scale for thickness. The data are also for a mean penetration depth of 2, but are extended to a thickness of ten times that value, twice the thickness shown in Fig. 6. The data follow exactly a straight line trend.
A mathematically equivalent technique is to plot on linear scales the natural logarithm of the transmission, or of the intensity, vs. depth. From Eq. 3, such a plot will be linear, with slope = - 1/D.
Before turning to the question of measurements that do not distinguish "main beam" from scattered and secondary radiation, we will describe the various sorts of events that actually do take place for photons incident upon matter:
For photons incident upon matter there is a chance that scattering will occur with the final photon having the same energy as the incident photon. This violates conservation of momentum and energy if we think of them as the same photon being bounced off of the atom. A more accurate semi-classical view of the situation is as follows:
The incident electromagnetic wave sets the atomic electrons vibrating (the energy being provided by absorption of the first few photons). The vibrating electrons, being accelerated charged particles, will radiate electromagnetic waves. (Recall the discussion of bremsstrahlung in the Chapter III section about X-ray machines.) Because of the sinusoidal vibration of the electrons, the radiated waves will be of the same frequency as the incident waves, and with a phase shift at the atom that depends on the binding of the electron. It is this "coherent," or "synchronized" scattering that gives rise to consistent interference effects such as are utilized in X-ray diffraction studies, as discussed in Chapter VIII. Because the maximum photon energy that can be absorbed without ionizing an atom is about 0.1 MeV, we do not expect to observe Thomson scattering at higher energies.
One of the ways electromagnetic radiation interacts with matter is known as the photoelectric effect, which is characterized by a photon giving all of its energy to an atomic electron, ionizing the atom in a single interaction. The photoelectric effect is therefore observed only for photon energies greater than the binding energy of at least some of the atomic electrons. The photoelectric effect is the dominant interaction of photons with matter, for those photons whose energy falls approximately in the range 1 keV < 
< 0.5 MeV. This includes virtually all dental and medical diagnostic X-rays, airport baggage inspection X-rays, and X-rays emitted during relaxation of the atomic electrons following radioactive nuclear decay.
In the case of solid or liquid metals, the atomic electron binding energy may involve two parts: first, for inner shell electrons, elevation of the electron to the conduction (valence) energy band, and second, ejection of a conduction band electron from the metal. For the higher photon energies typical of X-ray and gamma sources, we usually regard the binding energy as a single quantity, the total needed to remove the electron from the metal.
For ultraviolet or visible light, which does not penetrate deeply, the ejected electron will typically come from an atom near the surface of the target. The excess of the photon's energy beyond the binding energy of the electron is initially in the form of kinetic energy of the ejected electron. The electron may dissipate this energy within the metal, or it may fly off in some direction. In the case of a metal, as discussed above, it makes sense to think of an "initial kinetic energy" which is the excess of the photon's energy above that, if any, needed to elevate the target electron into the conduction band. Some of that energy is needed to break the electron free from the surface of the metal; this is the "work function" of the metal, as discussed in the next section.
for all x within the metal. The true U(x) is not flat, but it is periodic, because of the regular spacing of the nuclei (and inner-shell electrons, which together form the "atomic core") in the crystalline arrangement of the atoms. A quantum mechanical theorem shows that a periodic potential can be very effectively approximated by a flat one for many situations. The electrons do not generally leak out of the metal, they are held inside by a retaining force on the electron when it is at the surface, hence the slope of U(x) 
0 at the surface.
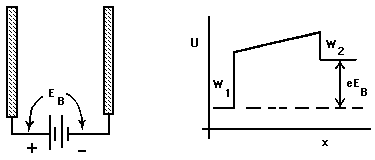
In Fig. 1 we take x = 0 as the surface. The energy that must be supplied just to overcome the binding of the electron to the metal, i.e., to move the electron from just inside the metal to just outside it, is W = 
- . W is known as the "valence electron binding energy" or "work function" of the metal. Experimental determinations of the work function are found to give results that are highly sensitive to the condition of the surface: impurities, corrosion, scratches, or anything else that alters the character of the outer few Ångstroms of the metal will influence the measured value of W.
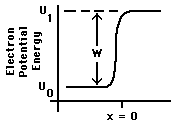
Figure 1: Potential Energy near a metal surface.
As discussed in conjunction with Fig. I-4, the slope of U(x) beyond the surface of the metal is determined by the electric forces, if any, on the electron when it is there. In the case illustrated here, U(x) is flat, indicating zero electric forces on the electron once it has escaped. Thus the slope outside the metal will depend on the net charges, if any, on that piece of metal and on any nearby objects. For example, if U(x) increases as the electron moves along, the kinetic energy of the moving electron will decrease, hence that would represent a retarding electric field.
, of metal 
is greater than the work function, 
, of 
. Then the graph of Fig. 2b will apply. The potential difference between the region just outside plate 1 and the region just outside plate 2 caused by the plates being in electrical contact through the shorting wire is known as the "contact potential difference" and is simply equal to the difference of their two work functions, - (see also Fisher and Varney, 1976).
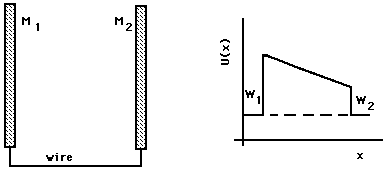
(a, cross section) (b)Figure 2: Two plates wired together.
The slope of U(x) in the region between the plates gives the force on the electron in the usual way; other geometries for the two metal pieces may give curved graphs of U(x) between the plates. In the illustrated case, an electron emitted with any kinetic energy from plate 1 will be accelerated by the electric field between the plates, moving toward plate 2 with increasing kinetic energy, where it will be absorbed with the transformation of its kinetic energy into heat. An electron emitted from plate 2 toward plate 1 will be slowed down by the electric field; if it has enough kinetic energy to begin with, it will be able to reach plate 1, where it will be absorbed. (An electron emitted from plate 2 with a velocity vector partly tangential to the plate surface will follow a curved trajectory and may not reach the other plate's surface, even if it has adequate energy.)
A battery or other power supply can be connected between the plates, forcing a particular difference between the potential energy of an electron within one plate and an electron within the other plate. This produces the situation illustrated in Fig. 3. The potential energy difference induced by the battery is e
, the product of the electron's charge, e, measured in Coulombs, and the potential of the battery, , measured in Joules/Coulomb (= Volts).
(a) (b)Figure 3: Two plates at different potentials.
Suppose that an amount of energy, , is suddenly given to an electron just inside the plate, by, for example, a photon. If is greater than , the electron may emerge from the surface with kinetic energy, T, as great as 
= - . T will be less than if some energy is transferred to other electrons within the metal as the ejected electron is on its way out. In the case illustrated in Fig. 3b, a sufficiently large T will permit the electron, if it starts out headed directly for the other plate, to reach the other plate, although it will be slowed down by the electric field in the space between the plates. The applied potential, , is therefore known in this case as the "retarding potential," sometimes with symbol 
.
Inspection of Fig. 3b, together with a little algebra, based on the above analysis, reveals that for any there is a critical retarding potential, 
, which is just barely sufficient to stop all of the electrons leaving plate 1 from reaching plate 2, regardless of the angle of their initial direction of travel. is known as the "stopping potential," and can be found as follows:
In the photoelectric effect, the energy is provided by a photon of light of visible or shorter wavelength; thus the "stopping potential," , provides a measure of the photon energy with an unknown but fixed offset, . The standard experiment uses light of multiple, specific different colors, and hence of multiple, different photon energies; changes in the photon energy are of interest, so for this purpose the fixed offset, , presents no problems.
where h is Planck's constant, and hence from Eq. 6,
where , the stopping potential, is as defined above, and discussed below.
The "gedanken experiment" requires simply the selection of a particular color of light and then adjustment of the retarding potential, , until the forward current stops (we define , the stopping potential, as this particular value of ). We regard as a function of the frequency, f, and see from Eq. 8 that it is a linear relation, with slope h/e. There will be a "threshold frequency," 
, below which no current will be observed for any positive value of . The threshold photon energy, = h*, will be equal to the greater of and .
Various frequencies may be obtained, for example, by placing selected filters, or filter combinations, in front of a mercury lamp and letting the filtered light fall on the target, for example a metal film cathode deposited on the inside surface of a glass vacuum tube photocell. In order to obtain a sharply defined wavelength, interference filters are frequently used. Interference filters are constructed as a stack of alternating layers of two different indices of refraction, designed so that the partial reflections will destructively interfere, and the partial transmissions constructively interfere at a specific wavelength, 
. They work properly only when the light beam is perpendicular to the outside glass surfaces, because otherwise the path length inside each layer will be longer, and therefore the selected wavelength will be longer. Perpendicular adjustment is readily achieved in practice, because the reflected beam of de-selected wavelengths will be visible unless it coincides with the incoming beam. The other difficulty with interference filters is that they will necessarily also select light of wavelengths /2, /3, etc.. It is necessary, therefore, to include a "broadband" filter in the optical path before the light reaches the photocell. This filter need not select any particular wavelength, i.e., its transmission can be a smooth broadly-peaked function of wavelength, but it must have very low transmission for light of all wavelengths shorter than perhaps 0.8 .
The ejected electrons are collected by an anode, typically a wire loop (to avoid a large surface that would catch light and consequently function as a photocathode). A variable retarding potential is applied between the photocathode and the anode. The current to or from the anode while it is being maintained at the specific potential is read on an electrometer, capable of indicating currents to picoamperes. For each filter, the experimenter seeks the maximum photoelectron energy, i.e., the minimum retarding potential between cathode and anode that will just prevent all photoelectrons from reaching the anode.
We must now confront a deviation from textbook simplicity. The difficulty is that light reflected from the cathode onto the anode produces photoelectrons that can "go the wrong way." A plot of anode current versus retarding potential displays both positive and negative anode currents. The retarding potential can be so great that no photoelectrons from the cathode reach the anode; however the photoelectrons from the anode are accelerated to the cathode and are measured as a positive current to the anode. (The slope of current vs. potential in this region is dependent on the resistance of the insulators and cables, and on the input impedance of the electrometer.) For retarding potentials nearly equal to the "stopping potential," the currents of electrons leaving the anode and reaching the anode will be comparable. Hence, the current will be observed to be zero when there are still some electrons reaching the anode from the cathode. The potential at which the current vanishes, then, is a lower limit for an experimentally determined stopping potential.
Hall and Tuttle (1971) demonstrate that a sensible estimate for the stopping potential can be obtained by plotting the square root of the magnitude of the current versus the retarding potential, for the data with negative current (cathode electron dominated) and extrapolating the linear portion of the graph to the zero current axis. This extrapolation will be fraught with opportunities for error and bias.
in the range 1 keV < < 0.5 MeV, the dominant interaction with matter is in fact the photoelectric effect. Experiments can readily be made with sample foils of various elements, all samples having the same thickness as measured in cm, in atoms/square cm, or in mg/square cm. Whichever approach is taken, there are two interesting results: first, for any one element, the absortion coefficient depends on photon energy, typically varying over several orders of magnitude from 1 keV to 1 MeV. Furthermore, the variation of the absortion coefficient is not smooth, but rather has smooth sections separated by discontinuities. In the smooth sections, the absortion coefficient decreases rapidly as photon energy increases, typically being proportional to the -7/2 power of the photon energy (see Marmier and Sheldon, 1969, section 4.4), for energies below 0.5 MeV, i.e., where the photoelectric effect dominates.
The discontinuities are sudden jump increases in the absortion coefficient as photon energy increases, but the overall trend is clearly for larger values of the absortion coefficient at lower energies. Second, there is a systematic variation among the elements in the photon energy at which those discontinuities are observed. This is the consequence of the variation of K and L shell binding energies with atomic number Z, as explored by Henry Moseley in his Nobel prize-winning research. That work involved emission spectroscopy, but the same atomic energy levels are responsible.
Although copper emits both 
and 
radiation, neither neutral copper atoms in any state, nor even copper ions in their ground state, can absorb these photons, because their absorption requires promotion of an electron from the K shell to the L or M shells, and both the L and M shells are completely filled. The photons have energy roughly equal to 9.9 keV, according to the Bohr model (see Eq. III-4), about 100 eV less than that needed to eject a K shell electron. In general, there will be a relatively small difference between a characteristic photon energy for an element and the minimum energy needed for a photon to be absorbable by ionizing the inner shell associated with that line.
A useful description is that the probability of absorption depends on the number of electrons capable of receiving the photon's energy (in essence, those electrons with binding energy smaller than the photon's energy). This explains the increased absorption seen in heavier elements (they have more electrons), and the fact that the absorption spectrum for any one element displays discontinuities at the binding energies of the several atomic electron shells. Photons of less energy than this "edge" can ionize only the outer electrons from the target atoms, but photons of greater energy can ionize both outer and inner electrons; hence the photons on the high energy side of the edge are much more strongly absorbed. Marmier and Sheldon (1969) show that the absorption is proportional to Z raised to the nth power, with 4 < n < 4.6, for photon energies between 100 keV and 2 MeV.
Because of the results mentioned in chapters I and III, from quantum mechanical perturbation theory, there is a resonance effect that causes a significant elevation of the probability of interaction, and hence of the value of , for energies just above the edge. Perturbation theory also provides an explanation for the general curving downward trend between edges: increased photon energy means that each possible interaction is farther "off resonance." The K edge energy depends on Z (see Eq. III-4), and is less than 0.15 MeV, for naturally occuring elements, hence we can expect the photoelectric effect to constitute a significant portion of the absorption only for photon energies well below 1 MeV.
An absorption discontinuity that can be observed when an X-ray beam produced with an accelerating potential of 30 kV is incident upon a copper absorber occurs at a wavelength of 0.138 nm, which is just shorter than the wavelength of the emission, as is discussed above. Therefore the photoelectric effect does occur, some photons in the primary X-ray beam have sufficient energy to ionize copper atoms. Further, for a copper anode, the value of the wavelength indicates that the incident photons must have originated as bremsstrahlung. A copper sample will exhibit the "absorption edge" when irradiated with a beam containing energies equivalent to 0.138 nm, regardless of the source. The discontinuity is thus characteristic of the absorber and is referred to as the CuK Absorption Edge. Since the elements in the periodic table have different energy-level structures and electron densities, one might expect to find an element which will specifically absorb Copper K emissions, by a systematic study of different elements.
Table I shows the 
and 
emission line wavelengths and the K edge absorption wavelengths for eight elements. The data in Table I confirm that for these transition metals, the K absorption edge of each of the elements listed has a wavelength between those of the and wavelengths of the element with atomic number larger by one. (At larger values of Z, the K absorption edge lies between the and lines of elements that differ by two or three in their Z values.) For example, cobalt foil absorbs both of the CuK emission lines, as does nickel, but nickel dramatically discriminates between the and radiation: although both and are absorbed by nickel, the is much more strongly absorbed by nickel than is the , so that the relative proportions of the two components of the beam shifts in favor of the . This technique is frequently used to "filter out" lines, in order to obtain a beam of more nearly monochromatic radiation.
Table I: Emission and Absorption Wavelengths(These values were transcribed from the TELTRON manual; they originated in the International Tables for X-Ray Crystallography)
Observe the discrepancy between atomic number order and atomic weight order for Cobalt and Nickel.
Element | Wavelengths (nm) | |||||
Emission | Absorption | |||||
| Atomic Number | Atomic Mass | Symbol | | | Mean | K edge |
|---|---|---|---|---|---|---|
| 23 | 50.94 | V | 0.255 | 0.228 | 0.242 | 0.227 |
| 24 | 52.00 | Cr | 0.229 | 0.208 | 0.2l8 | 0.207 |
| 25 | 54.94 | Mn | 0.2l0 | 0.191 | 0.200 | 0.189 |
| 26 | 55.85 | Fe | 0.194 | 0.176 | 0.185 | 0.174 |
| 27 | 58.93 | Co | 0.179 | 0.162 | 0.170 | 0.161 |
| 28 | 58.71 | Ni | 0.166 | 0.149 | 0.157 | 0.148 |
| 29 | 63.54 | Cu | 0.154 | 0.139 | 0.146 | 0.138 |
| 30 | 65.37 | Zn | 0.144 | 0.129 | 0.137 | 0.128 |
In 1913 and 1914 Henry Moseley used photographic diffraction methods to establish the wavelengths of the characteristic emission lines of all elements then known from aluminum to gold. At that time the periodic table of the elements was constructed in sequence of atomic weights, not as we now do, in sequence of atomic number, because there was as yet no way to establish the atomic number. Moseley found that the spectra followed a general law:
where 
is the wavelength of the spectral line, k and s are physical constants, and Z is an integer unique to the element (now known as the atomic number). Furthermore, for most of the elements, Z increased by one in passing sequentially through the periodic table, starting with Z = 1 for hydrogen. There were two classes of exceptions: first, a few elements were misplaced by one because the atomic weight sequence and the atomic number sequence differ (argon, cobalt, and tellurium); and second, a few values of Z were skipped, because those elements had not yet been discovered ( Z = 43, 62, 72, and 75; now known as Tc, Sm, Hf, and Re, respectively).
Moseley worked with characteristic emission spectra, so reproducing his work would require a set of X-ray tubes, each having an anode of different composition. This would be both expensive and time consuming. Absorption edge wavelengths are slightly different from, but just as discrete as, the emission wavelengths studied by Moseley; it is therefore sensible to simulate Moseley's work through an analysis of absorption edges.
For each element, the absorption coefficient depends on mass and on wavelength; where an absorption edge occurs there are two values of , a maximum and a minimum, for that particular wavelength. Characteristic radiation is emitted from the bombarded target only when the energy of the incident photon or electron is greater than or is equal to that of the corresponding absorption edge. Whenever an absorption edge is being observed there must be X-radiation present that is characteristic of the absorbing material; this radiation arises as the outer electrons "fall into" the vacancy created by the ejection of the inner-shell electron, and is emitted isotropically, and with wavelength always slightly longer than that of the incident radiation. It spreads in all directions, so weakens rapidly with distance from the point of impact on the target.
Another possible outcome of an interaction between an incident photon and an electron in the target material is an elastic collision in the classical billiard ball sense. This is known as the Compton effect in honor of Arthur Compton, who discovered it in 1923 (see Ford, 1974, pages 1068-71). In the simplest case, a free electron at rest is struck by a photon that scatters off at some angle to its original path. By the conservation of momentum and energy, the electron must recoil in a specific direction, with a specific energy. This energy must be provided by a reduction in the energy of the photon (increase in its wavelength). Although not emphasized in the previous discussion of the photoelectric effect, both that effect and the Compton effect require a target atom to recoil, in order to conserve the momentum vector (see Kidd, Ardini, and Anton, 1989).
In practice, of course, available electrons are usually bound to atoms, so that the approximation of a free, stationary electron is reasonably accurate when the photon energy greatly exceeds the binding energy of the electron. For X-ray photons and valence electrons this is certainly reasonable. As Kidd, Ardini, and Anton (1989) state, for 
, the Compton electron recoils approximately in the direction of the electric field vector of the incident light and Compton scattering merges smoothly into classical Thomson scattering in the limit of low frequency.
The probability of Compton scattering is typically small, but at energies around 1 MeV it is usually the most common interaction, because the photoelectric effect and pair production are even less likely. The probability of the photoelectric effect declines with increasing photon energy. Pair production, as described below, does not typically dominate until about 10 MeV.
One may readily view Compton scattering in terms of the energy loss, 
, or the wavelength increase, 
, as a function of 
, the angle between the initial and final photon directions. As a good approximation when small amounts of momentum and energy are transferred to the electron, the increase in the wavelength divided by the wavelength will be approximately equal to the decrease in energy divided by the energy. Examination of the algebra leads to the intuitively reasonable conclusion that the maximum momentum, and hence also the maximum energy, will be transferred from the photon to the target particle when the final photon travels in the opposite direction to the incident photon.
At photon energies above roughly 1 MeV another possibility becomes available when matter is struck by the photon: the creation of particle-anti-particle pairs. The lightest mass material particle (excluding neutrinos) is the electron; to make an electron and its anti-particle, a positron, requires twice the rest energy of an electron, since the positron is identical in mass to an electron. Thus the lowest energy at which pair production is observed is
Conservation of energy asserts that pair production will never be observed at lesser photon energy than given above. In fact, the probability is very small for photon energies appreciably less than about double the threshold, but it rises rapidly as the photon energy increases and becomes the dominant interaction for > 10 MeV. Observe that the fate of the electron created is identical to that of beta radiation of the same initial kinetic energy, as discussed in section C, below. The positron has the same fate as any other anti-particle: after gradually losing its kinetic energy (just as the electron does) it finds a natural particle (one of the atomic electrons in the target) and annihilates with it, producing two photons of energy equal to the electron rest energy, roughly 0.511 MeV. (As mentioned above, photons of this energy typically interact with matter by the photoelectric or Compton effects, and are fairly penetrating.)
We consider here two concerns alluded to in earlier comments on radiation measurements: the geometrical relationship between detected counting rate and source activity, and the relationship between source activity and the total number of nuclei present. With rare exceptions, the radiation emitted as a result of radioactivity will be isotropically distributed, including any X-rays emitted following the nuclear decay (as a part of the reshuffling of the atomic electrons in response to the change in the nucleus). Since the radiation is thus initially equally intense in all directions, we can easily relate the observed counting rate to the size of the detector and the separation, r, between it and the source; see Fig. 4.
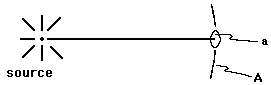
Figure 4: Detector Geometry; a = sensitive area of the detector, perpendicular to r. A = surface area of a sphere around the source with a radius of |r|.
The calculations are simplified for the case that the separation, r, is much larger than the source or detector diameters; this is normally the case. If the medium between the source and the detector is uniform, if this type of radiation is exponentially absorbed (as discussed earlier in this chapter, see Eqs. 1 through 4), and if we take I as the rate at which quanta are emitted by the nuclei of the source, then the rate at which quanta reach the sensitive area of the detector, after accounting for divergence from the source and for absorption in the intervening medium, will be as follows:
where D is the penetration depth (see the discussion following Eq. 4) for this type of radiation in this medium. If D >> r, it will be a good approximation that F(r) is proportional to 1/A, hence to 1/(
). In general it is also necessary to allow for a detection efficiency, E, that is less than one, so that the net counting rate will be:
or
where a is again the area of the detector, projected perpendicular to the line between the source and the detector, as shown in Fig. 4.
We have seen in section I of chapter I that a radioactive nucleus has a (generally small) probability per second, , of decaying. Hence the population of a collection of identical nuclei can be expected to decline according to the following formula:
The rate at which nuclei are decaying, which is minus the slope of the above curve, also declines, according to the related formula:
Since we know that the mean lifetime, 
, is the inverse of , we can collect expressions from Eqs. 13 and 15 to find that:
where the first factor involves characteristics of the radiation and the source, while the second factor involves characteristics of the detector, and its location.
When high energy charged particles move through matter, they interact with the atomic electrons and with the nuclei. These collisions can often sensibly be thought of as non-contact events mediated by the electrostatic (Coulomb) repulsion or attraction. The overall result when a beam of such particles passes through matter is a gradual reduction in the mean energy of the incident particles, as they slow down to thermal velocities, exhibiting a penetration "range" that depends primarily on the initial energy and the density of the absorber. Virtually no charged particles penetrate even half again as far as the range, unlike the exponentially penetrating photons, nearly 5% of which get beyond three times the mean penetration depth, D, according to Eq. 3.
The reduction in energy of the incident particles is accompanied by the creation of secondary radiation in three forms: target particles ejected from their original positions by the collisions; photons created by the acceleration of the various charged particles; and particle-anti-particle pairs created from energy, if there is enough energy available for such pair-production.
Recalling the lessons of classical physics, which at this qualitative level are not changed by relativity theory or by quantum mechanics, the principles of conservation of momentum and energy lead to the following statements:
Let us now apply those general rules for collisions to the specific cases of alpha, beta, and muon beams incident on matter. Alpha particles will transfer energy gradually to the atomic electrons, being deflected in each case by some small angle. If the path of the alpha happens to lie very close to an atomic nucleus it may well be scattered by a large angle, but only for the lighter elements will it transfer very much of its energy even then. Because the alpha is so massive in comparison to the atomic electrons, its acceleration vector will typically remain small, so the probability of bremsstrahlung photon emission is very small. In the case of very high energy alphas incident nearly "head on" to the nucleus, the closest separation of the alpha and the target nucleus may be less than a Fermi. In that case the scattering will be influenced by the strong nuclear forces as well as the Coulomb repulsion, and indeed nuclear transformations may occur.
Beta particles will be scattered to large angles by, and will transfer significant amounts of their energy to, atomic electrons, but those atomic electrons are then simply beta radiation! Contrary to the case for alphas, the acceleration vector in such collisions will often be (briefly) quite large, so secondary photon radiation by the bremsstrahlung process is quite common. Often those secondary photons will carry significant amounts of energy to depths or at angles well beyond the penetration ability of the betas themselves.
Muons, as discussed in section E of chapter I, are simply massive versions of electrons, so we expect the same interactions for them as for beta radiation. Their mass, however, is intermediate between the nuclear mass and the electron mass, so they will transfer somewhat less energy to atomic electrons and more to nuclei in collisions. Their greater mass will also reduce the acceleration vector's magnitude, so that they will be less likely to emit bremsstrahlung. As shown in Eq. I-9, they eventually undergo radioactive decay (mean lifetime = 2.2 microseconds), emitting a beta particle and two neutrinos whose kinetic energies total about 100 MeV.
As is the case for incident photons, pair production for incident charged particles does not occur unless the initial energy exceeds the threshold, and it remains rare until the initial energy is roughly double that minimum value.
As discussed in Chapter VIII, a beam of particles all having the same speed and direction of travel are described quantum-mechanically in terms of a plane wave, and the wavelength of that wave will depend on the particles' momentum (and therefore also on their energy). If the particles pass through a region of space ("scattering center") in which the potential energy is reduced, their kinetic energy and momentum will of course increase and thus their wavelength decrease. Consequently, after passing through this region the waves will be out of phase with those that passed on either side of it.
Several mathematical approaches are possible for predicting the observations to be expected following such an interaction. Essentially, the undisturbed (transmitted) portion of the quantum mechanical waves will interfere with the phase-shifted (scattered) portion. As a result, the probability of observing a particle, which is proportional to the absolute square of the wave function, will depend on direction from the scattering center: instead of all of them continuing in the original direction, some will do so and others will be scattered at some angle to the original direction of travel.
The Ramsauer effect refers to those special cases in which there is no disturbance of the wavefronts beyond the well. This is detected experimentally as a zero probability of scattering from the well (a "resonance in the transmission"). To understand how this is possible, consider the case of a rectangular well of uniform depth, as illustrated in Fig. 5. The stippled region has a uniform potential energy less than that outside it. The kinetic energy is therefore greater, and the planes of constant phase ("wave fronts") are therefore closer together in the interior of the well, separated by a wavelength less than the wavelength outside. If, as in the illustrated case, the depth of the potential well, the incident energy, and the length of the well combine to produce precisely an integer number of cycles of phase shift compared to the outside waves, then the waves passing through the well and emerging on the far side will be in phase with those that passed around it. In such a case, the interference between transmitted and scattered waves will be constructive along the original direction, and destructive in all other directions.
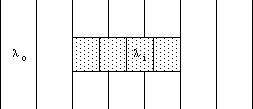
Figure 5: Simplified example of the Ramsauer Effect, showing wavelengths inside and outside the potential well.
An experiment to elucidate the Ramsauer Effect in the scattering of electrons from Xenon atoms can be performed using commercial "vacuum" tubes containing Xenon. The effective potential well presented to an incident electron by an atom of Xenon is spherically symmetric, but has a depth as a function of radius that is by no means simple to describe mathematically. The typical depth is perhaps 70 eV and the "resonant" energy for the incident electrons is less than 1 eV.
As the incident charged particles interact with the target material, they are slowed down and deflected in a variety of collisions. Each such change in velocity vector is the result of some brief period of acceleration, hence we expect some non-zero probability of the emission of photons of energy at most equal to the initial energy of the incident particles. The mechanism is identical to that involved in the production of continuous spectrum X-rays, see Chapter III, section B, under the name "Bremsstrahlung" (German for "braking radiation").
Secondary Bremsstrahlung is a particular hazard with incident light charged particles such as electrons and muons, because their small mass means that even reasonable forces will produce large acceleration vectors. The radiation is most likely to be emitted perpendicular to the original path, and will frequently be more penetrating than the original charged-particle radiation. Safety concerns for beta radiation, for example, are often dominated by the generation and absorption of such secondary photons.
Stable incident particles will typically deposit their initial kinetic energy gradually along their path through matter. In the case of alpha radiation, for example, this deposition is very nearly uniform. Unstable particles, such as muons and pions, will also deposit their decay energy in the matter, giving an overall effect of non-uniform deposition. For the treatment of massive deep tumors, this may be an advantage, provided that the pions can be given a well-defined initial energy such that they will arrive and stop in the middle of the tumor before decaying.
We can now understand a major difficulty in describing the beam of charged-particle radiation that penetrates to any given depth in a target:
This behavior is in sharp contrast to that of photons, as discussed in section B, where we saw that the count rate declines exponentially, but the photons remaining in the beam still have their initial energy. See Cember Fig. 5.4 for betas and Eqs. 5.13, 14, and 15 for alphas. As you might expect, the maximum range increases with increasing initial energy. Cember (pp. 108-113) also shows that the range of beta radiation in aluminum is roughly
R = (1 mm/MeV)*E
In other words, beta radiation will penetrate about 1 mm of aluminum for each MeV of initial kinetic energy. This is significant in light of the common usage of several cm of aluminum as a filter to remove low energy photons from medical X-ray beams with a peak photon energy of perhaps 200 keV: very few of the secondary betas, whether ejected by Compton or photoelectric events, will reach the patient.
One can establish a minimum thickness of shielding needed to offer protection from a radiation source. For photons, Eq. 13, above, provides a reasonable basis. For charged particles, the thickness needed must exceed the range, based on the initial energy and type of particle. These simply established minimum shielding thicknesses are inadequate in practice because of the fact that secondary radiation (either deflected main-beam particles or newly created radiation) will be headed in different directions and may even be more penetrating. For example, as mentioned above, secondary photons are produced by beta radiation. These photons are exponentially absorbed, and therefore some will surely penetrate father than the maximum range of the beta radiation that produced them!
In some cases the secondary radiation from a primary beam may cause more total energy deposition/micron than the original beam itself. Cobalt-60 gamma rays (or any other photons of about 1 MeV) are of this type. It takes a few millimeters of tissue to build up the full intensity of secondary radiation, hence it is "skin-sparing" when used to treat deep tumors. If it is used to treat surface lesions, there must be a "tissue phantom," typically a plastic bag filled with water, on top of the true tissue surface. In the case of very high energy radiation, such as cosmic rays in space or the output beam of an experimental particle physics accelerator, it may require several inches of solid lead to absorb the secondary radiation back down to the point that it is merely as damaging as the initial beam! It is for this reason that the space shuttle and the space station are not constructed with radiation shielding: the secondary radiation from any shielding that could be carried into orbit would be worse than the primary radiation. They do, however, stay in low Earth orbit, taking advantage of the Earth's magnetic field to deflect most of the charged-particle radiation away (forming the van Allen radiation belts) at higher altitudes.
The key idea here is to plan radiation shielding on the basis of practical experience. By now, of course, a great deal has been learned and summarized in published articles and handbooks. If such are not available, the minimum requirement is to have available utterly excessive shielding for a radioactive source and an on-off switch for an artificial source, together with suitable detectors to monitor the remaining radiation with a proposed shield. Be aware that significant scattering of radiation can occur from the air molecules within and from walls around a room.
If the incident radiation is anti-matter (or if pair production has created secondary anti-matter), there will be secondary (or tertiary) gamma radiation. Whenever an anti-matter particle lingers in the vicinity of its regular matter counterpart, they annihilate each other. That is, their mass is transformed into radiant energy. This interaction must conserve energy and momentum, so in the center of momemtum, "c.o.m.," frame of the pair there must be two photons of opposite momentum vector, each having equal energy in that frame. In the c.o.m. frame, each photon has energy equal to the rest energy of the particle (or anti-particle, since their masses are exactly equal) plus half of the total kinetic energy in the c.o.m. frame.
Like the electron and positron, particle and anti-particle will in general have opposite charges (or both be neutral), so they will not repel each other. Thus, the annihilation of anti-matter with regular matter is to be expected for all anti-matter particles. If high energy incident radiation of any form has undergone a pair production reaction, then the ultimate effect will include the gradual loss of kinetic energy of each created particle, through collisions, followed by the annihilation of the anti-particle with a regular particle already located at the resting place of that anti-matter. The consequent gamma radiation will have energy of 0.511 MeV for electrons, more for any other type of particle, and so will be highly penetrating.
Trial Time (sec) Counts R(cm) r(cm)
A 10 264,605 11.77 12.17
B 10 48,072 23.79 24.19
C 10 21,496 31.92 32.32
R = distance to aperture whose diameter = 0.375 inch
r = distance of air traversed from source to detector
efficiency of detector = 0.806 (transmission through light-tight paper)
background = 100 counts in 10 sec
a) What are I(0) and D? A graphical analysis is sensible.
b) How accurately are the three rates determined?
c) How accurately are I(0) and D determined from these data?
Dick Piccard revised this file (https://people.ohio.edu/piccard/radnotes/penetrate.html) on November 26, 2024.
Please E-mail comments or suggestions to piccard@ohio.edu.